Cross multiplication – Examples and Formula

In this lesson we will learn about cross multiplication, and also learn in brief how to useful cross multiplication to solve the problems.

To understand the cross multiplication first we see the parts of a fraction.  

 Parts of a fraction

We know that a fraction has a division bar and two numbers. One number above the division bar and other number is below the division bar.

The number above the division bar is the numerator. 

and the number below the division bar is the denominator.

Cross multiplication is useful for a few different purposes.

For example: We can compare fractions and find out which fraction is bigger or greater.

When we do it, make sure that we start with the numerator of the first fraction.

In cross multiplication:

1. We multiply the numerator of the first fraction with denominator of the second fraction.

2. The numerator of the second fraction with denominator of the first fraction.

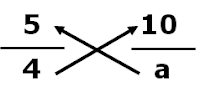
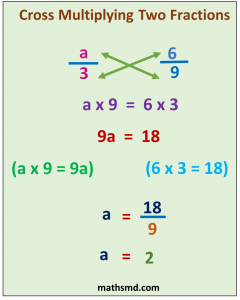
Example – Simplify fraction 5/4 = 10/a
                               5/4 = 10/a
Solution:

Step 1:     Cross multiply 

we multiply the numerator of the first fraction, with denominator of the second fraction and the numerator of the second fraction, with denominator of the first fraction.

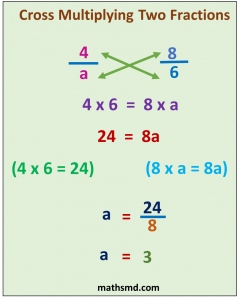
                           5 x a = 10 x 4

Step 2.  Multiply 5 to a on left side and 10 to 4 on right side.

                               5a = 40

Step 3. Isolate variable a

                              a = 40/5

a = 8

Answer: a =8.

Comparing fractions with cross multiplication

Unlike fractions can be compared with the help of cross multiplication.

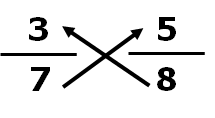
Example: Compare 3/7 and 5/8 using cross-multiplication.

Step 1: Here are two fractions 3/7 and 5/8, have different denominators, so compare two fractions with different denominators we make their denominators same. 
We change it by product of both of the denominators.

Step 2: So, the denominator of both the fractions becomes 7 x 8 = 56

Now we find the numerators of both fractions by cross multiplication. 

1. First we multiply the numerator of the first fraction with the denominator of the second fraction.

Numerator of the first fraction is 3 and denominator of the second fraction is 8, so multiply 3 x 8 = 24.

So, the first fraction becomes 24/56.

2. Now multiply the numerator of second fraction is 5 and denominator of the first fraction is 7, so multiply 5 x 7 =35.

 And the second fraction becomes 35/56.

Since 35/56 > 24/56

Therefore, 5/8 > 3/7.

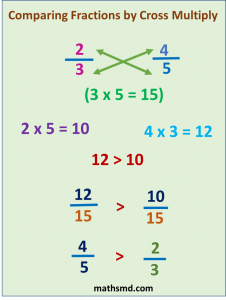
Example: Compare 5/4 and 3/2.

Using cross multiplication we find,

                   5 x 2 = 10, and 3 x 4 = 12.

Since, 12 > 10,

Therefore, 3/2 > 5/4.

Example: Compare 3/5, 5/8 and 6/7.

We want to compare three fractions, and find out which of them is the greatest.

Cross multiplication works with only two fractions at a time, so pick the first two fractions.

3/5 and 5/8

Using cross multiplication we find,

3 x 8 = 24, and 5 x 5 = 25.

Since, 25 > 24,

Therefore, 5/8 > 3/5.

Now 5/8 is greater than 3/5, so we can throw out 3/5, and do same thing for 5/8 and 6/7.

Using cross multiplication we find,

5 x 7 = 35, and 6 x 8 = 48.

Since, 48 > 35,

Therefore, 6/7 > 5/8.

Answer: 6/7 > 5/8 > 3/5

Using cross multiplication, we can solve equations, involving ratios.  

We can solve an equation with two ratios, using cross multiplication and find the value of the variable.

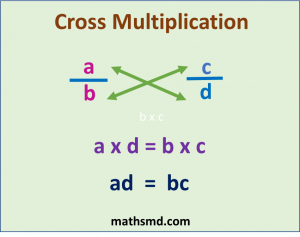
The equation a/b =c/d

It means to multiply the numerator of one fraction by the denominator of the other fraction. 

We multiply numerator a, of faction a/b to the denominator d of other fraction c/d, then 

                         a x d = ad

              multiplication will be ad.

Similarly, we multiply numerator c, of faction c/d to the denominator b of other fraction a/b, then

                           b x c = bc

              multiplication will be bc.

                 Therefore, ad = bc

Where b and d are not equal to zero.
Similarly, y and n are not equal to zero.
and q and s are not equal to zero. 

ad = bc, Similarly xn = ym, and ps = qr.

Note:

1. A fraction with a zero denominator is undefined.

2. A fraction with a zero numerator equals to zero.