Surface Area and Lateral Surface Area 

Cuboid 

In our day life, when we look around the room in our house we can see may things that has a shape of rectangular box. We use many box shaped objects, like a shoe box, a book a TV etc.

The shape of all these objects have same, or all these objects are made of six rectangular planes, this shape is known as Cuboid.

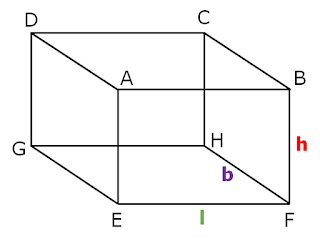
A cuboid is a closed three dimensional figure with length, breadth and height.

It has six rectangles and each rectangle called the face.

In above figure ABCD, EFGH, ADGE, BCHF, ABEF and DCGH are six faces of cuboid.

The top face ABCD and bottom face EFGH are opposite pair of cuboid.

ADGE and BCHF are pairs of opposite faces, and also ABEF, DCGH are pairs of opposite faces.

ABEF-ADGE, BCHF- DCGH, ABEF-BCHF are adjacent faces of cuboid.

Edges: A line segment between any two adjacent vertices is called the edge of cuboid.

There are 12 edgs, in cuboid they are AB, AE, EF, BF, BC, CH, HF, DC, GH, DG, AD, GE.

Opposite sides of a rectangle are equal.

    so,        AB = DC = EF = GH,

                AD = BC = GE = HF,

  and         AE = BF = CH = DG.

Vertex: The point where three edges of a cuboid are meet is called vertex.

A cuboid has eight vertices A, B, C, D, E, F, G, H, are vertices of cuboid.

 Surface area of a cuboid

The sum of the areas of the six rectangles is the Surface area of a cuboid.

If we take the length of the cuboid as l, breadth as b and the height as h then,

(1)   area of rectangle ABCD = l x b
(2)   area of rectangle GHEF = l x b

(3)   area of rectangle ADGE = b x h
(4)   area of rectangle BCHF = b x h

(5)   area of rectangle ABEF = l x h
(6)   area of rectangle DCGH = l x h

Total Surface area of a cuboid = The sum of the areas of the six rectangles.

                            = 2(l x b) + 2(b x h) + 2(l x h

= 2(lb) + 2(bh) + 2(lh)

Total Surface area of a cuboid = 2(lb + bh + lh)

Where l, b and h are three edges of the cuboid respectively. 

Surface Area of a Cube

A cuboid whose length, breadth and height are equal, is called a “Cube.

length = breadth = height 

If each edge of the cube is ‘a’ then the 
Surface Area of a Cube = 

(1)   area of square ABCD = a x a
(2)   area of square GHEF = a x a

 (3)   area of square ADGE = a x a
 (4)   area of square BCHF = a x a

(5)   area of square ABEF = a x a
(6)   area of square DCGH = a x a 

                                   = 2(a x a)
                                   = 2(a x a)
                                   = 2(a x a)
                                   = 2a² + 2a² + 2a²

                 Surface Area of a Cube = 6a² 

Lateral Surface area of a Cuboid

 When we find only area of the four faces, leaving the bottom and top face then the area of these four faces is called the lateral surface area of cuboid.

(1)  Area of rectangle ADGE = b x h
                       +
 (2)  Area of rectangle BCHF = b x h
                       +(3)   Area of rectangle ABEF = l x h
                       +
(4)   Area of rectangle DCGH = l x h

So, lateral surface area of a cuboid of length l, breadth b and height h is equal to,

= (b x h) + (b x h) + (l x b) + (l x b)

= 2bh + 2lb

= 2(b + l)h

or,   = 2(l + b)h.

Lateral Surface Area of a Cuboid = 2(l + b)h

Similarly,

Lateral surface area of a cube

Lateral surface area of a cube of side a is equal to,

^{Lateral Surface Area of a Cube} = 4a²