Odd numbers

Definition: If any integer that can not divide exactly by 2, is an odd number. Simply, If we divide any integer by 2, and remainder is one, we get an odd number.

The last digit of odd numbers is 1, 3, 5, 7, 9, 11…

Example: 11, 23, 35, 47, 69, all are odd numbers.

 Odd number properties

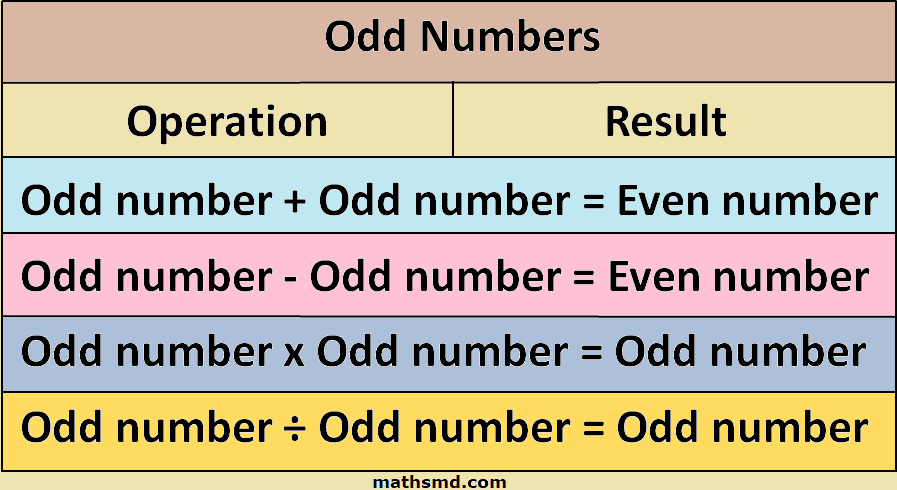
Addition: The addition of two odd numbers always gives an even number, i.e., the sum of two odd numbers is always an even number.

Example: 5 (odd) + 7 (odd) = 12 (even)

Subtraction: The subtraction of two odd numbers always gives an even number, i.e., When an odd number is subtracted from other odd number, the result is always an even number.

Example: 9 (odd) – 7 (odd) = 2 (even)

Multiplication: Multiplication of two odd numbers always gives an odd number.

Example: 3 (odd) x 5 (odd) = 35 (odd)

Division: Division of two odd numbers always gives an odd number.

Example: 39 (odd) ÷ 3 (odd) = 13 (odd). 

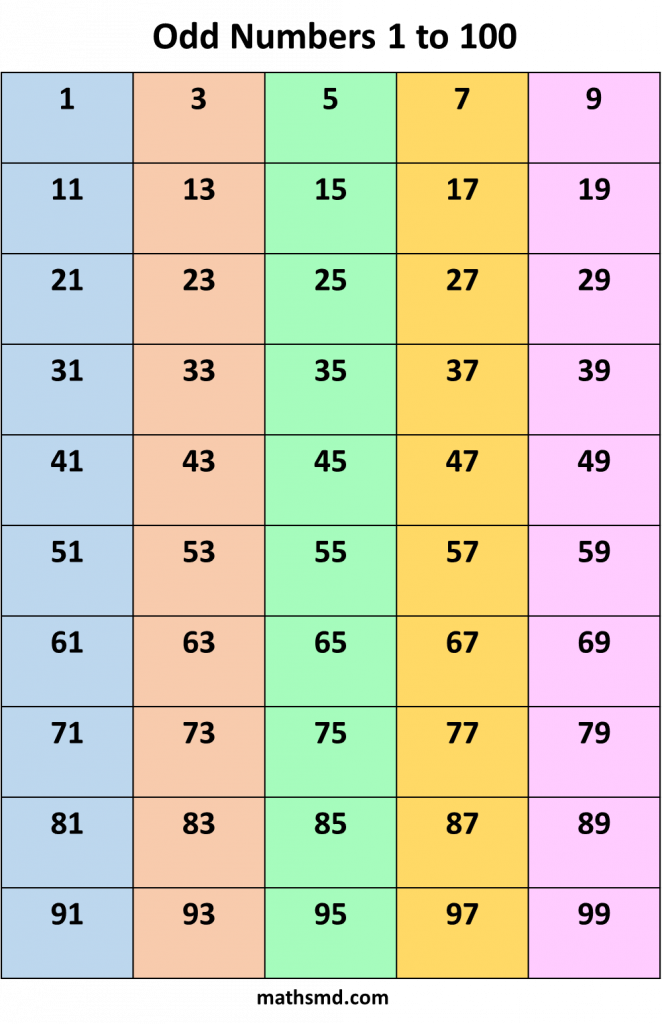
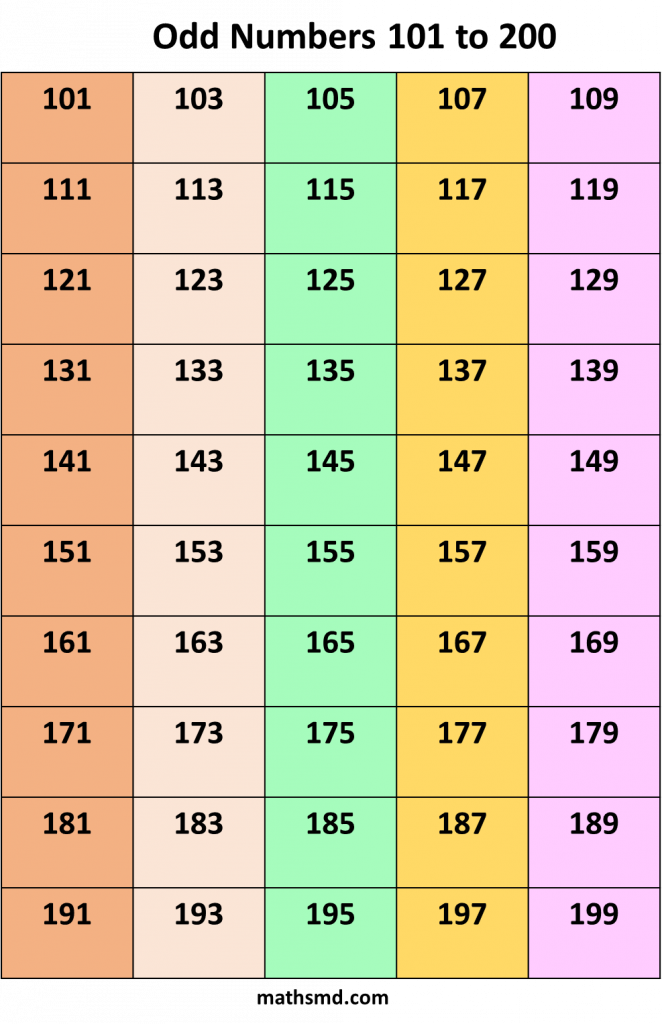
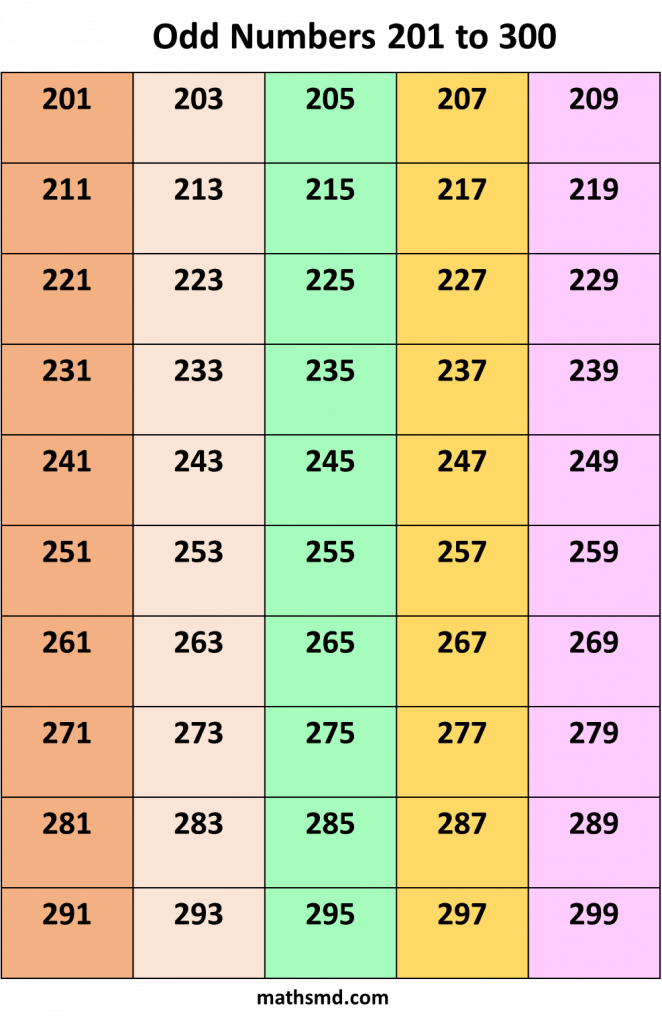
Odd numbers From 1 to 1000

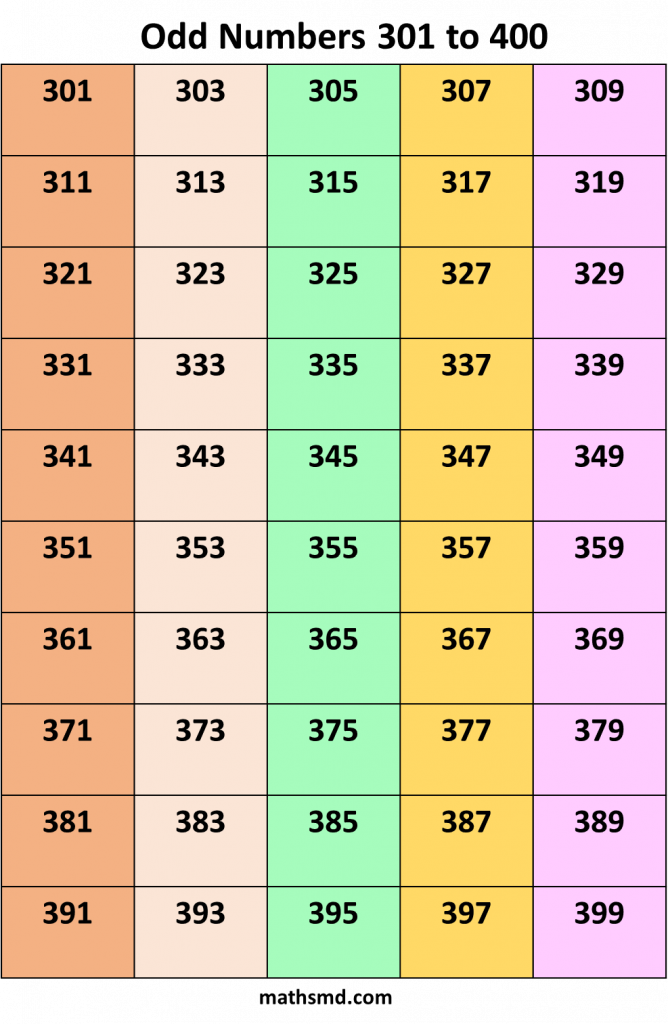
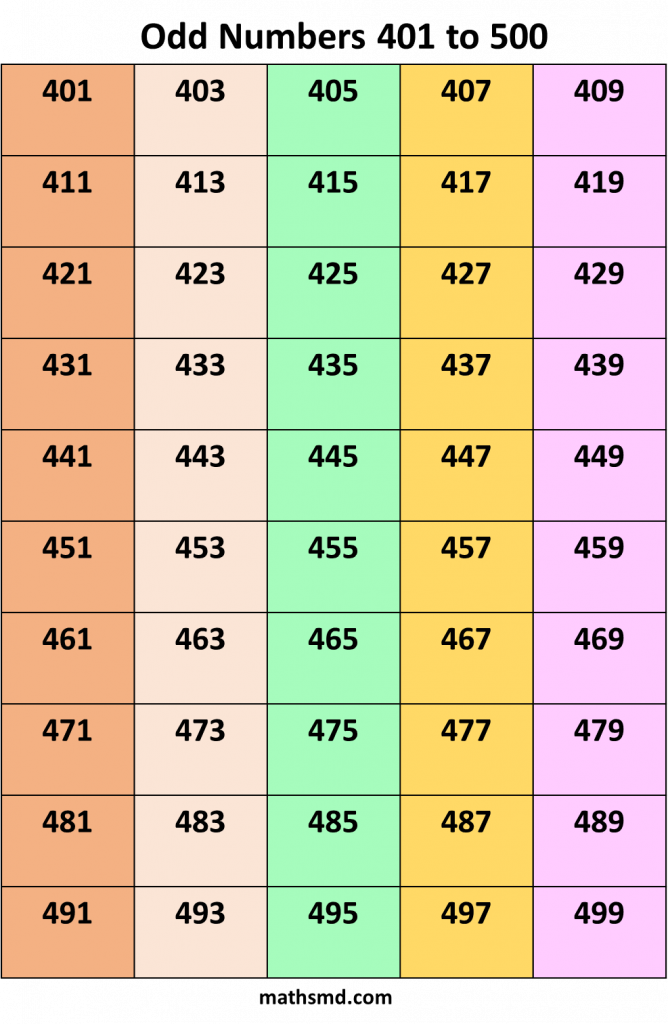
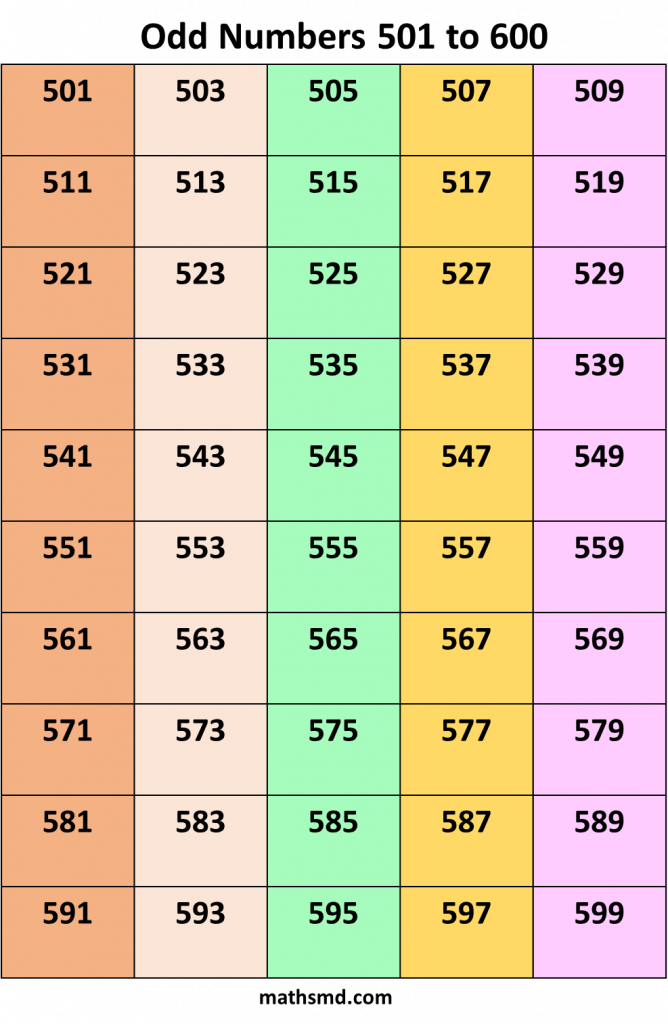
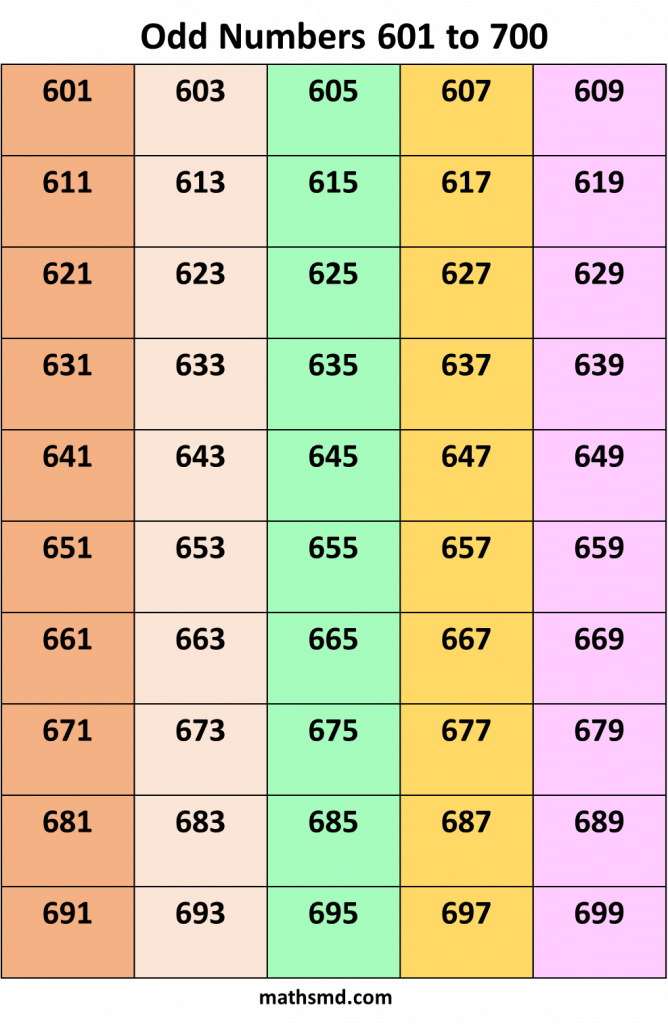
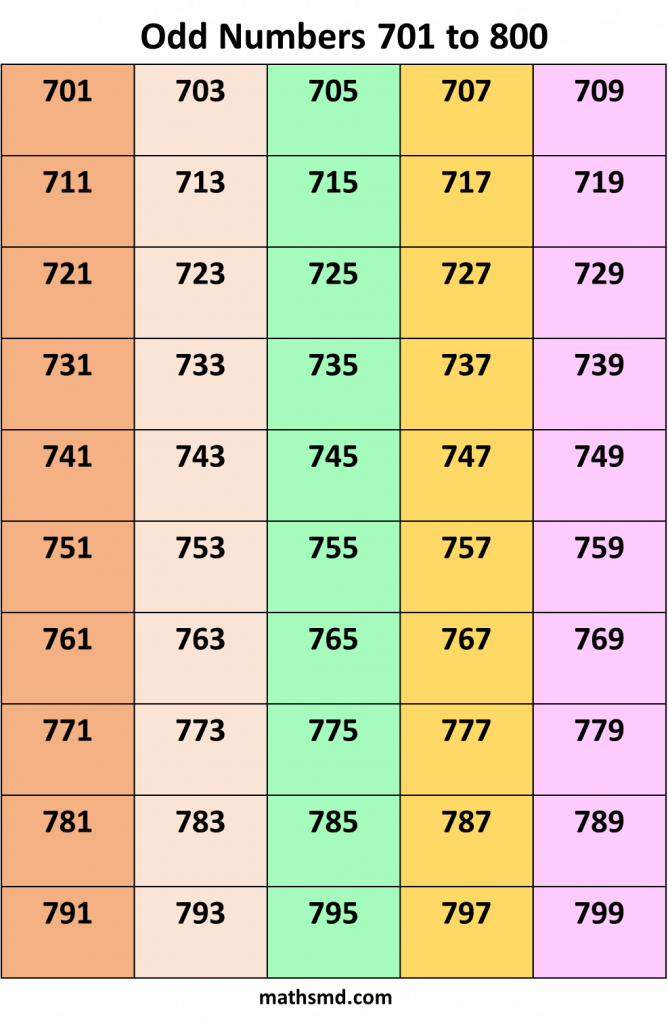
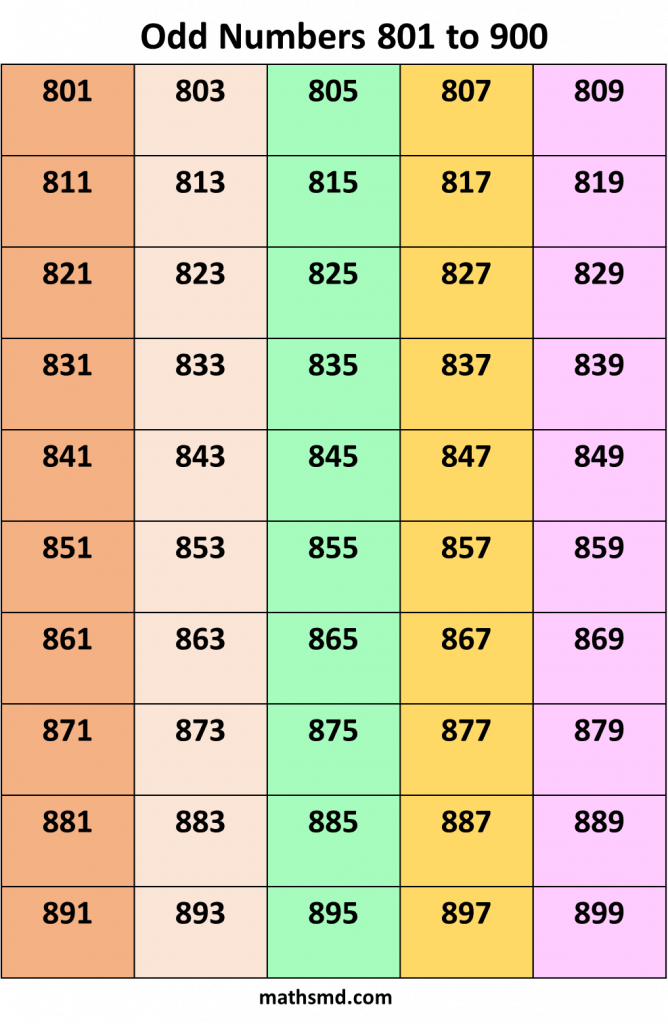
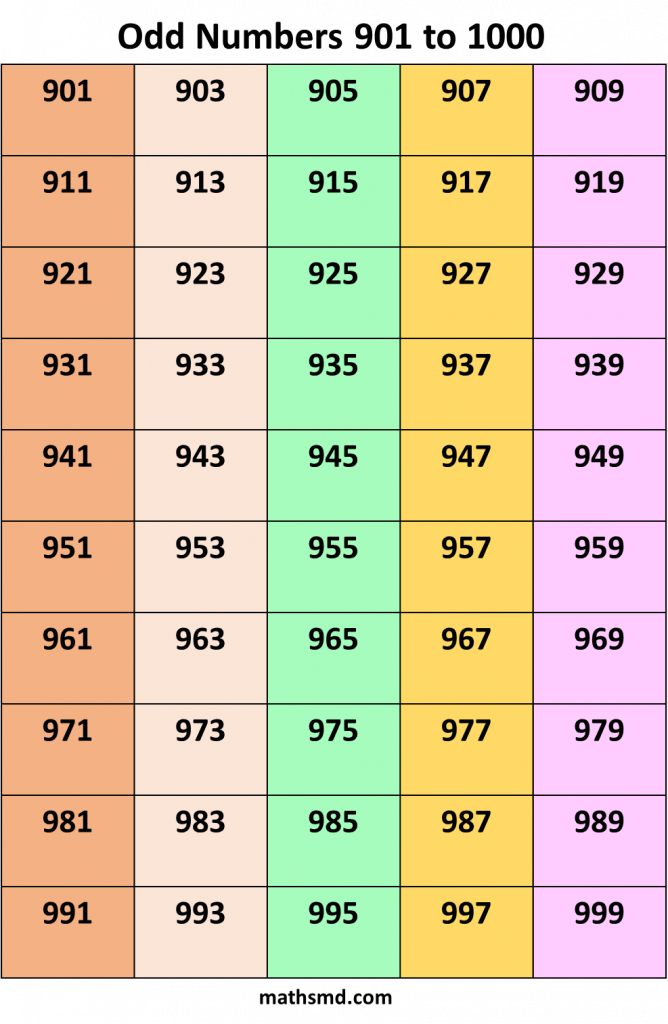
Odd number + Odd number = Even number

Odd number – Odd number = Even number

Odd number x Odd number = Odd number

Odd number ÷ Odd number = Odd number

1. Addition property of even and odd numbers.

Operation	Example	Result
Even number + Even number	2 + 4 = 6	Even
Even number + Odd number	8 + 3 = 11	Odd
Odd number+ Even number	5 +10 = 15	Odd
Odd number + Odd number	3 + 5 = 8	Even

2. Subtraction property of even and odd numbers.

The same thing happens when we subtract instead of adding.

3. Multiplication property of even and odd numbers.

Operation	Example	Result
Even x Even	2 x 4 = 8	Even
Even x Odd	8 x 3 = 24	Even
Odd x Even	5 x 10 = 50	Even
Odd x Odd	3 x 5 = 15	Odd

1	2	3	4	5	6	7	8	9	10	11	12
Odd	Even	Odd	Even	Odd	Even	Odd	Even	Odd	Even	Odd	Even

1	3	5	7	9	11
Odd	Odd	Odd	Odd	Odd	Odd