What is an Acute Triangle: Definition, Formula and Properties

In geometry, a triangle is a polygon with three sides, three vertices and three interior angles. In other words a triangle is a closed two dimensional plane figure with three sides and three angles.

Triangles are classified on the basis of their sides and angles. There are many types of triangles and an acute triangle is one of them.

Acute Angle Definition

If all the interior angles of a triangle are less than 90 degree, then the triangle is known as an acute triangle.

An Acute triangle have no angles greater than are equal to 90⁰ (degrees).

An acute triangle is classified on the basis of the measurement of angles.

Classification of acute triangles on the basic of their angles is as follows.

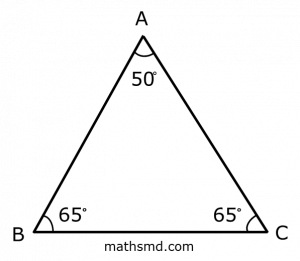
Equilateral Acute Triangle: In an equilateral acute triangle, all three sides are equal and all three interior angles are equal to 60º.

In an equilateral triangle, measure of all three angles is 60º (less than 90º) making it an acute triangle.

Isosceles Acute Triangle: In an isosceles acute triangle, measure of two sides and two interior angles are equal and all interior angles are less than 90.

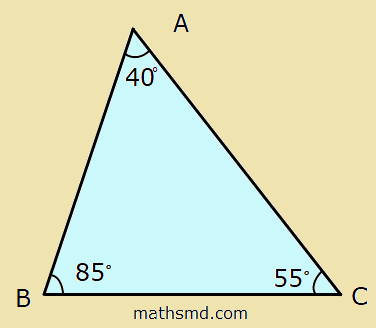
Scalene Acute Angle: In an scalene acute triangle, all the three sides are different length and all interior angles are different in measure, but all the interior angles measure less than 90º.

Triangle ABC is an scalene acute triangle because all three angles ∠A, ∠B and ∠C are acute angles or no angles greater than are equal to 90⁰ (degrees).

Properties of Acute Triangles

There are few properties of an acute triangle.

The sum of all three interior angles of an acute triangle 180º.

The line drawn from the base of the triangle to opposite vertex is always perpendicular.

At a same time a triangle cannot be a right-angled triangle and an acute- angled triangle.

At a same time a triangle cannot be a obtuse-angled triangle and an acute- angled triangle.

The interior angles of an acute triangle are always less than 90º or lie between (0º an 90º).

The smallest side of the triangle is opposite to the smallest angle.

Area of a Acute Angle

Area of Acute Triangle

The area of a acute triangle = (1/2) x base x height.

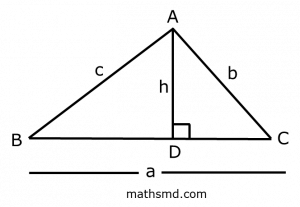
Here, BC denotes the base and AD denotes the height of an acute triangle.

Perimeter of a acute triangle

Perimeter of an acute triangle is equal to the sum of the length of the sides of a triangle.

Perimeter of a acute triangle = a + b+ c

Where a , b and c are sides of given triangle.

Semi Perimeter of the triangle = (a + b+ c)/2

Where S is the semi perimeter of the triangle.