Proportion

When two ratios or (fractions) are equal, then they are in Proportion.

A proportion is an equality of ratios.

The symbol “::” or “=” to equal represent the two ratios.

               It can be written in two ways

1. Colon form

2. Fractional form

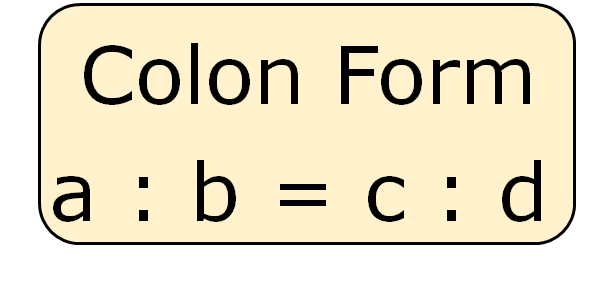
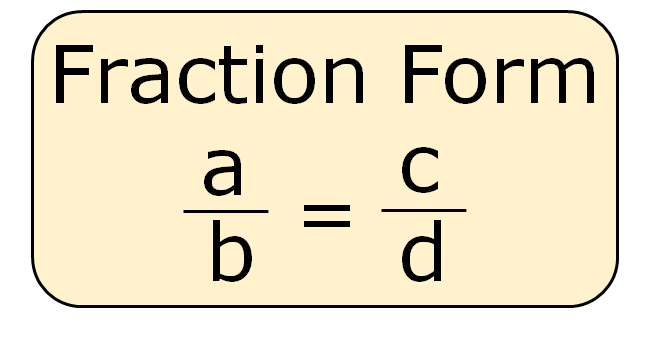
The terms a, b, c, and d are known as the terms of the proportion.

Both can be read as “a is to b and c is to d”.

a :b : : c : d, a, b, c and are the first, second, third and fourth terms of proportion respectively.

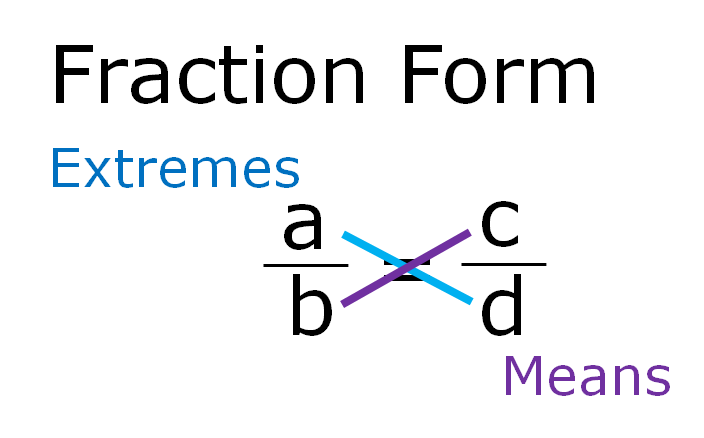
The first and fourth terms a and d are called extremes or extreme terms and the second and third terms b and c are called means or mean terms (middle terms).

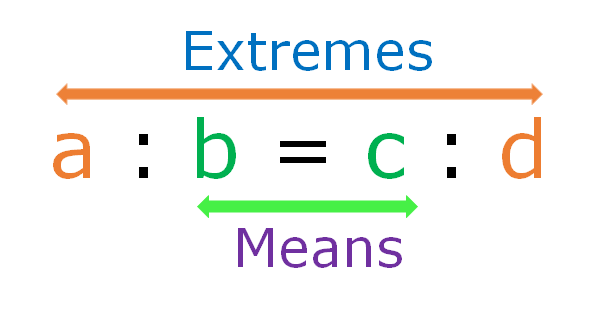
Mathematically, if four quantities a, b, c, and d are in proportion, then the ratio a : b must be equal to c : d.
i.e. a : b = c : d

The product of extremes = The product of the means

i.e. ad = bc (The cross product rule)

Proportion can include numbers or variables or both.

How to solve Proportions?

If given ratios are proportional, it is easy to calculate.

Step 1: Multiply first term with the fourth term: a x d

Step 2: Multiply second term with the third term: b x c

Step 3: If the product of extreme terms is equal to product of mean terms, then the ratios are proportional
i.e. a x d = b x c

1. Using a colon     a : b = c : d
2. Two equal fractions  a/b = c/d 

When two ratios are equal then there cross              product, of the ratios are equal.

Therefore,  a : b = c : d,   a x d = b x c

The ratios 15/25 and 3/5 are proportional and are write as

The ratio 15/25 = 3/5

is read as fifteen is to twenty five as three is to five.

Example: when we say that 4, 5, 40 and 50 are in proportion which is written as  

4 : 5 :: 40 : 50

and read as 4 is to 5 as 40 is to 50

or written as  4 : 5 = 40 : 50

4/5 = 40/50

cross product of ratios is 

4 x 50 = 5 x 40

200 = 200

both are equal.

Example: we can say 2, 3, 10, and 15 are in proportion which is written as
                             2 : 3 :: 10 : 15

and read as 2 is to 3 as 10 is to 15.

or written as 2 : 3 = 10 : 15

2/3 = 10/15

cross product of ratios is 

2 x 15 = 3 x 10

30 = 30, both are equal.

Here, the cross products are not equal, so this shows that the ratios are not in proportion.

When ratio is 3 : 5 and 4 : 7

Check the cross product of the given ratios.

3 x 7 = 4 x 5

The products are 21 and 20.

Here, the cross products are not same, so this ratios are not in proportion.

21 ≠ 20, This shows that ratios are not in proportion.

When ratio is 5 : 4 and 8 : 7

Cross product 5 x 7 = 35, and 8 x 4 = 32.

Here, the cross products are not same, so this shows that the ratios are not in proportion.

Find the third proportion to 6 and 12.

Let the third proportional be c

Then, b² = ac

(12)² = 6 x c

144 = 6 x c

c = 144/6

c = 24

Find the mean proportion between 5 and 45.

Let the mean proportion between 5 and 45 is p.
apply formula b² = ac

Therefore, p x p = 5 x 45 = 225

(p²) = 225

p = 15

Hence, the mean proportion between 5 and 45 is 15

How to tell two ratios are in form a proportion

First method: Same scale used on top and bottom

Here we see that a scale 5 used on top and bottom both, because multiply both 6 and 7 by same number this is a proportion.

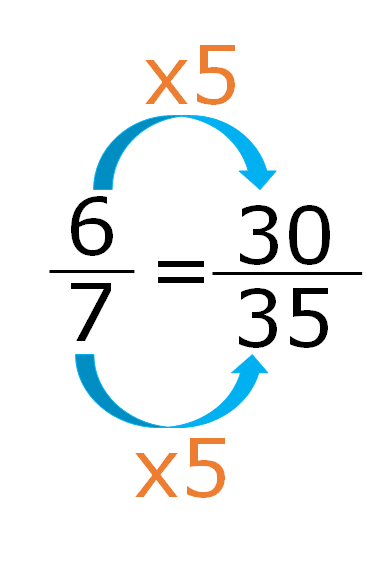
Second method : Simplify ratios

In this example, we divide the ratio 30 : 35, by 5 and we see that the ratios are equivalent. Therefore, they are in the proportional form.

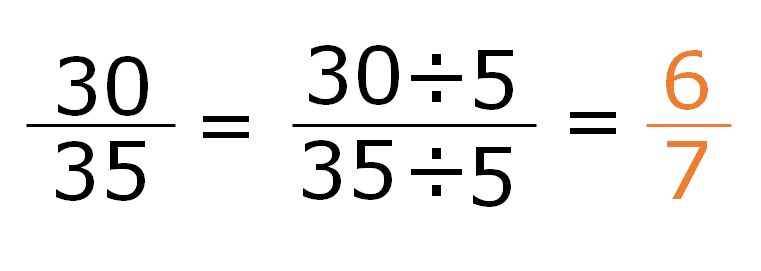
Third method : Cross product

In cross product method we multiply the numbers that are diagonal to each other, if the products are equal, the two ratios form a proportions.

3 x 12 = 36 and 4 x 9 = 36

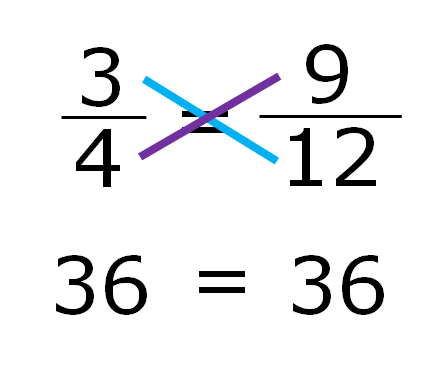
Example: Solve k/20 = 5/4

Apply cross multiplication we get

k x 4 = 5 x 20

4k = 100

k = 100/4

k = 25

Example: Solve 3/12 = 5/k

Apply cross multiplication we get

3 x k = 12 x 5

3k = 60

k = 60/3

k = 20

Continued proportions

Three quantities a, b, and c are said to be in continued proportion if a: b = b : c.

The term c is called the third proportion of a and b, and b is called the mean proportion of terms a and c.

In fractional form ab = bc,

Here, we see that b² = ac.

Verify the ratio 3 : 6 :: 6 : 12 is proportion.

This is continued proportion, therefore the formula

a x c = b x b

Here, a : b : c = 3 : 6 : 12

Multiply first and third terms

3 x 12 = 36

square of middle term = (6²) = 36

Therefore, the ratio 3 : 6 : 12 is in proportion

If two ratios are equal, then their reciprocals must also equal as long as they exist.

Reciprocal of a/b = c/d ⇨ b/a = d/c

a/b = c/d ⇨ a x d (Product of extremes) = b x c (Product of means)