Surface Area of a Right Circular Cone – Definition – Formula – Example 

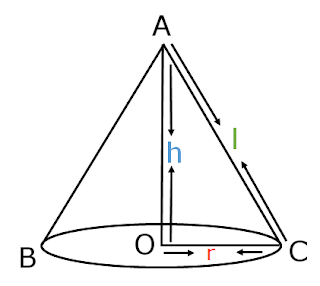
                        Right Circular Cone 

Definition: 

(1)  The surface area of a cone is sum of area of its base and lateral(side) surface.

(2)  The Lateral Surface Area of a cone is area of its lateral or side surface.

In above figure, 
A is called vertex, AO is height,  OC is radius,
AC is slant height of cone.

The height, radius, and slant height of the cone are usually denoted by h, r, l, respectively.

Formula: The formula of 

(1) Curved (Lateral) Surface Area = 𝝿rl

r stand for radius of circular base and l stand for slant height.

(2) Total surface area = 𝝿r² + 𝝿rl
Total surface area = 𝝿r(r + l)

(3) l² = r² + h²

Here h is height of cone so by applying Pythagoras theorem,
                         l = √r² + h²

Example: (1) Find the curved surface area of a right circular cone whose slant height is 12 cm and base radius is 7 cm.

Solution: Here, slant height of cone, l = 12 cm

and base radius of cone, r = 7 cm so, put the value in formula

              Curved surface area = 𝝿rl

                                            = (22/7) x 7 x 12 

   Curved surface area of cone = 264 cm²

Example: (2) Find the curved surface area of a right circular cone whose slant height is 21 cm and base radius is 10 cm.

Solution:  Here, slant height of cone, l = 21 cm

and base radius of cone, r = 10 cm so, put the value in formula

              Curved surface area = 𝝿rl

                                            = (22/7) x 10 x 21

                                            =22 x 10 x 3

                                            = 660

   Curved surface area of cone = 660 cm²

Example: (3) Find the curved surface area and total surface area of a right circular cone whose height is 16 cm and base radius is 12 cm.

Solution: Here, height of cone, h = 16 cm and 
                                 radius, r = 12 cm

                   so from,  l² = r² + h²

                                  l = √r² + √h²

= √12² + 16²

= √400

                                    = 20

 so, Curved surface area = 𝝿rl

                                    = 22/7 x 12 x 20

                                    =  22 x 12 x (20/7)

=753.6 cm²

Curved surface area of cone = 753.6 cm²

∴ Total surface area of cone = 𝝿rl + 𝝿r²

= 753.6 + (22/7) x 12 x 12 

 = 753.6 + 452.16 = 1205.76 cm2 

∴ Total surface area of cone = 1205.76 cm2 

Example: (4) Find the curved surface area and of a right circular cone whose slant height is 10 cm and diameter of the base of the cone is 10 cm.

Solution: Here diameter 2r = 10 cm

                  ∴              r = 10/2 

                                    = 5 cm

                    slant height = 10 cm

so,  Curved surface area = 𝝿rl                                   

= (22/7) x 5 x 10

                                    =  22/7 x 5 x 10

                                  =1100/7

                                    = 157.14 cm²
∴ Curved surface area of cone = 157.14 cm²

Example: (5) Find the curved surface area and total surface area of a right circular cone if it’s slant height is 21 cm and diameter of base is 24 cm.

Solution: Here slant height l = 21 cm
            Diameter of base 2r = 24 cm                                                 ∴  radius r = 12 cm

so,  Curved surface area = 𝝿rl

                                    = 22/7 x 12 x 21

                                    =  22 x 12 x 21_                                               7                                    = 1100/7

                                    = 157.14 cm²

Total surface area of cone = 𝝿r(r + l)

   = (22/7) x 12 (21 +12)

                                       = (22/7) x 12 x 33

                                       = 1244.57 cm²

∴ Total surface area of cone = 1244.57 cm2 

Example: (6) Curved surface area of a cone is 616 cm2, if it’s slant height is 14 cm.
Find total surface area and radius of the base of a right circular cone.

Solution: Curved surface area of cone = 616 cm²
                                     l = 14 cm
                                     r = ?
         Curved surface area = 𝝿rl

                                616 = 22/7 x r x 14

                                616 = 22 x r x 2

                                616 = 44 x r   

                              ∴    r = 616/44 

                                    r = 14 cm

Hence base radius of cone = 14 cm.      
Total surface area of the cone = 𝝿r (l + r)

                                            =22/7 x 14 (14 + 14)

                                            = 22 x 2 x 28

                                            = 1232  cm²

 Total surface area of the cone  = 1232 cm²