Place Value – Charts – Definition, Facts, Examples, With Solutions

What is Place Value

We across all time various numbers consists of digits. Digits may be one digit or two digits, three digits or many more. As the name suggests, Place Value is related to the position or place.

The value of each digit in a number depending on the position or place. This value is known as place value.

Definition:

The place value is define as the position or value of each digit in a number.

In Indian place value system, The place value chart separated in groups known as periods i.e. ones, thousands, lakhs, crores and Arab and so on.

The order of place value of digits in a number from right to left is ones(units), tens, hundreds, thousands, ten thousands, lakhs, ten lakhs crore and so on.

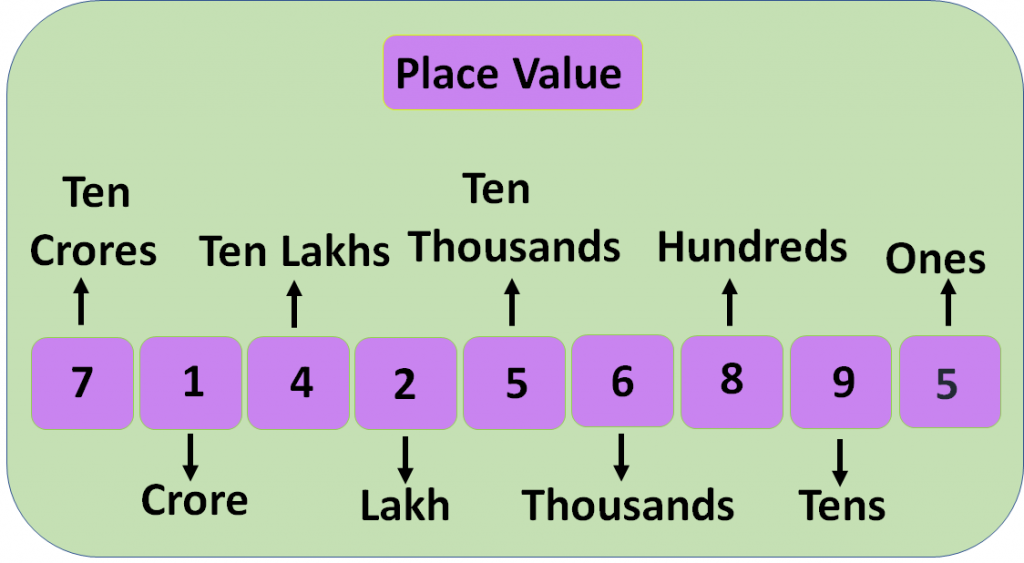
The value of each digit in any number is depending on its place or position.

Place Value Explanation

We know main counting numbers from 0 to 9. These are use to express all other numbers.

These positions start from a unit place or ones position, called one’s position.

1	Place-1	1 Digit	Ones
2	Place-2	2 Digits	Tens
3	Place-3	3 Digits	Hundreds
4	Place-4	4 Digits	Thousands
5	Place-5	5 Digits	Ten Thousands
6	Place-6	6 Digits	Lakhs
7	Place-7	7 Digits	Ten Lakhs
8	Place-8	8 Digits	Crore
9	Place-9	9 Digits	Ten Crores

We start with place 1,

place 1 has only one digit,

place 2 has 2 digits,

place 3 has only 3 digits and so on.

There are no digits on the right side of 1. So this place 1 is called ones.

Now 1st place is filled and we need to go for 2nd place, as 10 has 2 digits, so 2nd place is started at 10, where 1 is in the place 2 and 0 is in the place one.

This place 2 is called tens.

Third digit is started at 100, where 1 is in the place 3 and 0 is in place two and one.

This place is called hundreds. This process is going on.

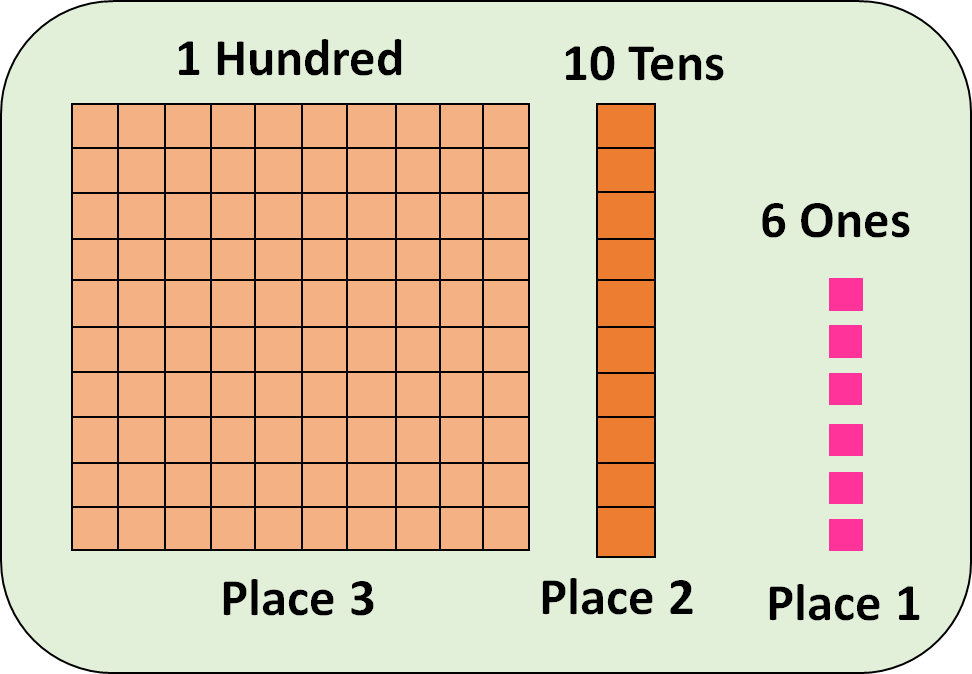
In mathematics, place value describes the position of a digit in a number. When a number in a general form, we will expanded the position of each digit.

How to calculate Place Value

(i) The value is calculated by multiplying the digit by the value of its place or position.

(ii) It is determine as ones , tens, hundreds, thousands.

Example: Let’s take a number 346. In the number 346, every digit have different values.

Here, we note that in the number 346, “6” is in the ones place or position, so the value of 6 is ones.

“6” is in the ones position, so the value of 6 is

6 x 1 = 6

 “4” is in the tens position, so the value of 4 is tens.

“4” is in the tens position, so the value of 4 is

4 x 10 = 40

 “3” is in the hundreds position, so the value of 3 is hundreds.

and “3” is in the hundreds position, so the value of 3 is

3 x 100 = 300

Hundreds	Tens	Ones
3	4	6

                   The place value of 3 is 300.

                   The place value of 4 is 40.

                   The place value of 6 is 6.

                   This also can be written as 

                    3 x 100 + 4 x 10 + 6 x 1

 Example: In the number 785, “5” is in the ones position, so the  value of 5 is 5 ones, “8” is in the tens position, so the value of 8 is 8 tens and “7” is in the hundreds position, so the value of 7 is 7 hundreds.

“5” is in the  ones position, so the value of 5 is

5 x 1 = 5

“8” is in the tens position, so the value of 8 is

8 x 10 = 80

“7” is in the hundreds position, so the value of 7 is

7 x 100 = 700

Hundreds	Tens	Ones
7	8	5

The place value of 7 is 100.

The place value of 8 is 80.

The place value of 5 is 5.

This also can be written as, 

7 x 100 + 8 x 10 + 5 x 1

Place Value of Zero

The place value of zero in any number is always zero. Zero may be any place of the number, but its value will be zero. In numbers 250, 309, 2304, 15402, the place value of 0 in each number is 0.

Zero may stand for nothing, but that doesn’t mean we can leave them out.

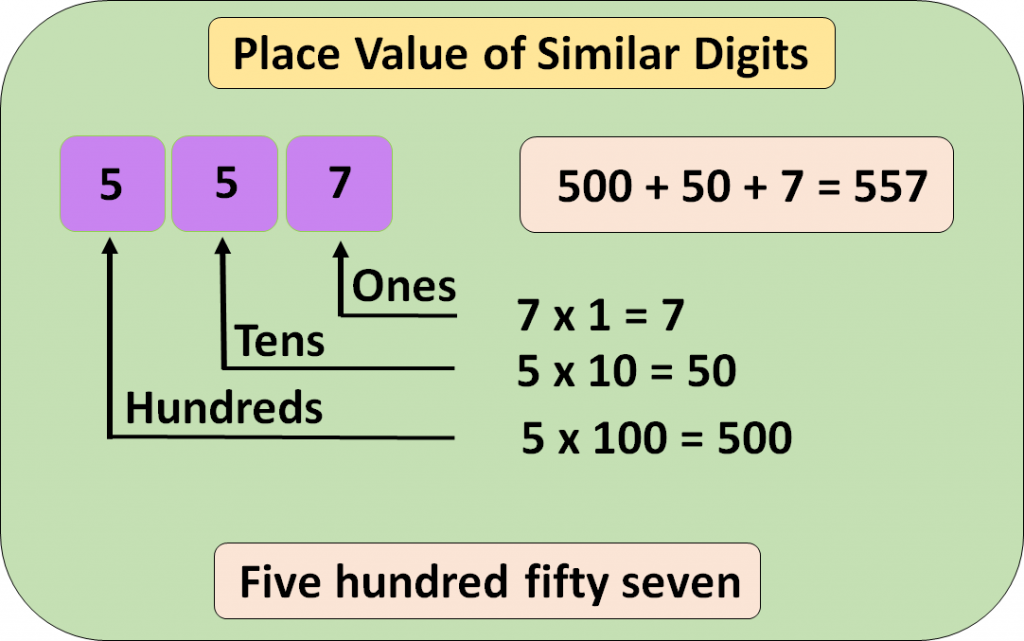
Place Value of Similar Digits

A number have two similar digits but different values, which is decided by the position of digit holds in the number.

Example: Let’s take a number 557. Here we note that the digit 5 is used twice in this number. Both 5 have a different value. Place value is defined as the numerical value of each digit in a number depending on its position or place.

So the place value of left most 5 is hundreds and the one in the center is tens.

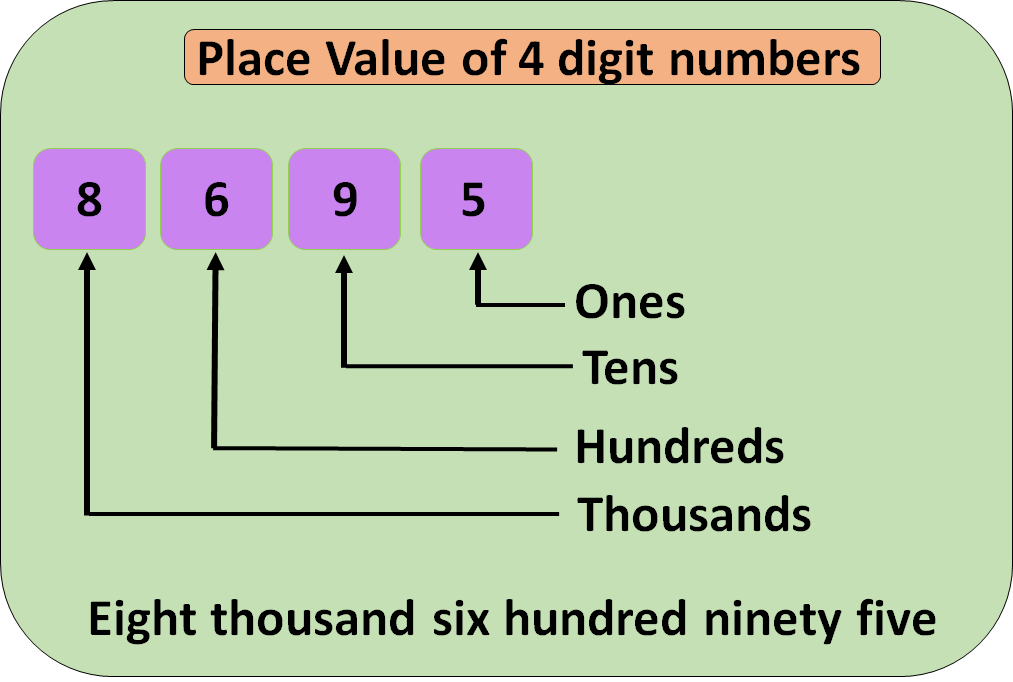
Example: In Number 6234, 4 represents 4 ones, 2 represents 2 tens, 3 represents 3 hundreds and 6 represents 6 thousands.

Thousands	Hundreds	Tens	Ones
6	2	3	4

In Number 8695, 5 represents 5 ones, 9 represents 9 tens, 6 represents 6 hundreds and 8 represents 8 thousands.

A Place value chart shows how many hundred tens and ones are use.

Each period has a hundreds, tens and ones position.

Large whole numbers are arranged in groups of three places. Each group called period, commas are usually used to separate the periods.

Indian Place Value Chart

Number	Place Value	Value of Digit
97,85,14,236	One’s	6
97,85,14,236	Ten’s	30
97,85,14,236	Hundred’s	200
97,85,14,236	Thousand’s	4,000
97,85,14,236	Ten Thousands	10,000
97,85,14,236	Lakh	500,000
97,85,14,236	Ten Lakhs	8,000,000
97,85,14,236	Crore	7,00,00,000
97,85,14,236	Ten Crores	90,00,00,000

International Place Value Chart

Number	Place Value	Value of Digit
98,514,236	One’s	6
98,514,236	Ten’s	30
98,514,236	Hundred’s	200
98,514,236	Thousand’s	4,000
98,514,236	Ten Thousands	10,000
98,514,236	Hundred Thousand	500,000
98,514,236	Millions	8,000,000
98,514,236	Ten Millions	90,000,000

In International place value system, The place value chart separated in groups known as periods i.e. ones, thousands, millions and so on.

Place Value Chart

Example: Find the place value of all digits in the number; 5836

Thousand	Hundreds	Tens	Ones
5	8	3	6

Solution: The digit 6 is the ones place, so, the place value of 6 is 6 x 1 = 6

The digit 3 is the tens place, so, the place value of 3 is 3 x 10 = 30

The digit 8 is the hundreds place, so, the place value of 8 is 8 x 100 = 800

The digit 5 is the thousands place, so, the place value of 5 is 5 x 1000 = 5000

Example: Find the place value of all digits in the number; 91235

Ten Thousand	Thousand	Hundreds	Tens	Ones
9	1	2	3	5

Solution: The digit 5 is the ones place, so, the place value of 5 is 5 x 1 = 5

The digit 3 is the tens place, so, the place value of 3 is 3 x 10 = 30

The digit 2 is the hundreds place, so, the place value of 2 is 2 x 100 = 200

The digit 1 is the thousands place, so, the place value of 1 is 1 x 1000 = 1000

The digit 9 is the ten thousands place, so, the place value of 9 is 1 x 10000 = 10000

Example: In the number 653498, write the digit that is in
(i) One’s place (ii) hundred’s place (iii) hundred thousand’s place (iv) ten thousand’s place

Solution: (i) One’s place is 8

(ii) hundred’s place is 4

(iii) hundred thousand’s place is 6

(iv) ten thousand’s place is 5

Example: What is the place value of 5 in 675

Solution: The place value of 5 in 675 is ones.

What is the place value of 6 in 675

Solution: The place value of 6 in 675 is hundreds place i.e. 6 x 100 = 600.

Example: What is the place value of 8 in 87

The place value of 8 in 875 is ones.

What is the place value of 4 in 649375.

Solution: The place value of 4 in 649375 is ten thousands.

4 x 10000 = 40000

Example: Expand the number 649375.

Lakh	Ten Thousand	Thousand	Hundreds	Tens	Ones
6	4	9	3	7	5

Solution: Expanded form of 649375 = 6 x 100000 + 4 x 10000 + 9 x 1000 + 3 x 100 + 7 x 10 + 5 x 1

649375 = 600000 + 40000 + 9000 + 300 + 70 +5

Example: What is the place value of 0 in 707

Solution: The place value of 0 in 707 is tens.

Example: Expand the number 2746385.

Ten Lakhs	Lakh	Ten Thousand	Thousand	Hundreds	Tens	Ones
2	7	4	6	3	8	5

Solution: Expanded form of 2746385 = 2 x 1000000 + 7 x 100000 + 4 x 10000 + 6 x 1000 + 3 x 100 + 8 x 10 + 5 x 1