Octagon – Definition – Shapes – Types – Formula – Properties

What is an Octagon?

An octagon is a geometric shape that falls within the category of polygons, specifically an eight-sided polygon. The term “octagon” is derived from the Greek words “okto,” meaning eight, and “gonia,” meaning angles.

Below is a detailed exploration of octagons:

Definition

An octagon is defined as a polygon with eight sides and eight angles. Each of the sides connects at vertices (corners) to form eight interior angles.

Types of Octagons

Octagons can be classified into two main types:

regular and irregular.

Octagons can be classified based on the equality of their sides and angles:

1. Regular Octagon:
   • Sides: All eight sides are of equal length.
   • Angles: All interior angles are equal, each measuring 135°.
   • Symmetry: It has symmetrical properties, including rotational and reflection symmetry.
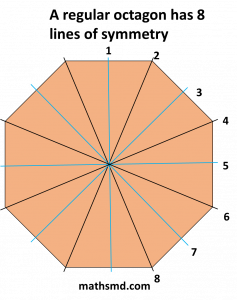
   • A regular octagon has 8 lines of symmetry.
   • It also has rotational symmetry of order 8.

Example: The stop sign is a common example of a regular octagon.

Irregular Octagon:

• Sides: The lengths of the sides are not equal.
• Angles: The interior angles are not necessarily equal.
• Symmetry: Lacks the symmetrical properties of a regular octagon.

Example: Many natural and man-made structures can form irregular octagons, like some floor tiles or decorative elements.

Formulas

1. Perimeter of a Regular Octagon

The perimeter (P) is the sum of all its sides. P=8a

where a is the length of one side.

2. Area of a Regular Octagon

The area (A) can be calculated using the following formula:

A=2(1+√2)a²

where a is the length of one side.

Alternatively, the area can also be calculated using the apothem (the perpendicular distance from the center to a side):

A=1/2×P×apothem

Properties of Octagons

1. Interior Angles:

• The sum of the interior angles of any octagon can be calculated using the formula: Sum of interior angles=(n−2)×180º
• For an octagon (n=8):
• Sum of interior angles=(8−2)×180∘ = 1080º
• In a regular octagon, each interior angle is: Each interior angle=1080/8=135º

2. Exterior Angles:

• The sum of the exterior angles of any polygon is always 360°.
• In a regular octagon, each exterior angle is: Each exterior angle=360/8=45º

3. Diagonals:

• The number of diagonals in an octagon can be calculated using the formula: Number of diagonals=n(n−3)/2
• For an octagon: Number of diagonals=8(8−3)2=20
• A regular octagon has 8 lines of symmetry.
• It also has rotational symmetry of order 8 (i.e., it looks the same after a rotation of 45º or any multiple of 45º.

Applications and Examples

• Architecture and Design: Octagonal shapes are often used in architecture, such as in buildings, towers, and decorative elements.
• Road Signs: The stop sign is a notable example of a regular octagon.
• Games and Puzzles: Many board games and puzzles use octagonal pieces or boards.
• Flooring: Octagonal tiles are common in flooring and other interior designs.

Summary

An octagon is a versatile and interesting polygon with eight sides and eight angles. Its properties, such as the sum of its interior angles, number of diagonals, and symmetrical characteristics, make it a fundamental shape in geometry. Understanding octagons provides a foundation for exploring more complex geometric shapes and their applications in various fields.