Trigonometric Ratios: A Detailed Explanation

Trigonometric ratios are the ratios of the lengths of sides in a right-angled triangle. These ratios are fundamental in trigonometry and are used to relate the angles of a triangle to the lengths of its sides.

There are six primary trigonometric ratios.

sine, cosine, tangent, cosecant, secant, and cotangent.

Here’s a detailed explanation of each, along with their relationships and applications.

Basic Trigonometric Ratios

Consider a right-angled triangle with one of the non-right angles labeled as θ. The sides of the triangle relative to θ are,

• Opposite side: The side opposite to the angle θ.
• Adjacent side: The side next to the angle θ that is not the hypotenuse.
• Hypotenuse: The side opposite the right angle, which is the longest side of the triangle.

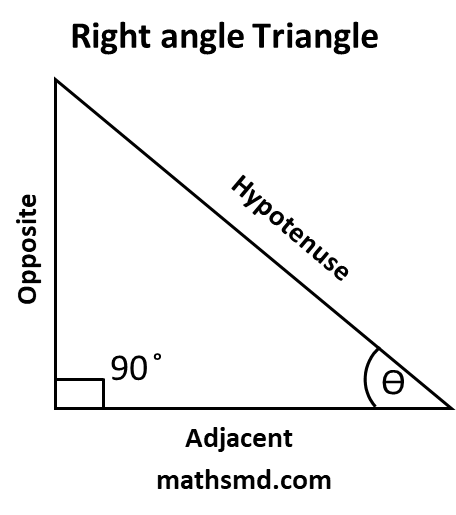
1. Sine (sin⁡)

The sine of an angle is the ratio of the length of the opposite side to the hypotenuse.

sin⁡(θ)=opposite/hypotenuse

2. Cosine (cos⁡)

The cosine of an angle is the ratio of the length of the adjacent side to the hypotenuse.

cos⁡(θ)=adjacent/hypotenuse

3. Tangent (tan⁡)

The tangent of an angle is the ratio of the length of the opposite side to the adjacent side.

tan⁡(θ)=opposite/adjacent

Reciprocal Trigonometric Ratios

These ratios are the reciprocals of the basic trigonometric functions.

4. Cosecant (csc⁡)

The cosecant of an angle is the reciprocal of the sine.

csc⁡(θ)=1/sin⁡(θ)=hypotenuse/opposite

5. Secant (sec⁡)

The secant of an angle is the reciprocal of the cosine.

sec⁡(θ)=1/cos⁡(θ)=hypotenuse/adjacent

6. Cotangent (cot⁡)

The cotangent of an angle is the reciprocal of the tangent.

cot⁡(θ)=1/tan⁡(θ)=adjacent/opposite

Relationships Between Trigonometric Ratios

Trigonometric ratios are interrelated through various identities and relationships.

Here are some important ones:

Pythagorean Identities

These identities are derived from the Pythagorean theorem and relate the squares of the trigonometric functions.

1. sin⁡2(θ)+cos⁡2(θ)=1
2. 1+tan⁡2(θ)=sec⁡2(θ)
3. 1+cot⁡2(θ)=csc⁡2(θ)

Co-function Identities

These identities relate trigonometric functions of complementary angles (angles that add up to 90∘).

1. sin⁡(90∘−θ)=cos⁡(θ)
2. cos⁡(90∘−θ)=sin⁡(θ)
3. tan⁡(90∘−θ)=cot⁡(θ)
4. cot⁡(90∘−θ)=tan⁡(θ)
5. sec⁡(90∘−θ)=csc⁡(θ)
6. csc⁡(90∘−θ)=sec⁡(θ)

Applications of Trigonometric Ratios

1. Solving Right Triangles:
   • Given one angle and one side, or two sides, you can find the remaining sides and angles using trigonometric ratios.
2. Modeling Periodic Phenomena:
   • Trigonometric functions model periodic phenomena such as sound waves, light waves, and tidal patterns.
3. Engineering and Physics:
   • Trigonometry is used to analyze forces, oscillations, and wave motion, among other physical concepts.
4. Navigation and Surveying:
   • Trigonometric ratios help determine distances and angles in navigation and land surveying.
5. Architecture and Construction:
   • Ensuring structures are built accurately and safely often requires calculations involving trigonometric ratios.

Unit Circle Representation

The unit circle is a powerful tool for understanding trigonometric ratios. It is a circle with a radius of 1 centered at the origin of a coordinate plane.

• Any angle θ corresponds to a point (x, y) on the unit circle
• where, cos⁡(θ)=x and sin⁡(θ)=y
• This representation extends the definitions of trigonometric ratios to all angles, not just those in a right triangle.

Summary

Trigonometric ratios (sin⁡, cos⁡, tan⁡, csc⁡, sec⁡, cot⁡) are fundamental in relating the angles and sides of triangles, particularly right-angled triangles. They have extensive applications in various fields, including physics, engineering, and navigation. Understanding these ratios and their interrelationships is crucial for solving geometric problems and modeling real-world phenomena. The unit circle provides a comprehensive framework for extending these ratios to all angles and visualizing their behavior.