Vertical Line: Definition, Formula, Equation, Properties and Examples
Vertical Line: Definition, Formula, Equation, Properties and Examples
What is a Vertical Line?
French Mathematician Rene Descartes trying to solve the problem of describing the position of a point on a plane with the Cartesian coordinate system and the cartesian plane.
In Cartesian coordinate system, we derive a vertical and a horizontal line. When we plot a point on a plane surface, we take two axes
(1) Y-axis-Vertical and
(2) X-axis-horizontal lines are drawn on a plane.
Y axis is called the vertical line.
Definition:
In a coordinate plane, a straight line goes from top to bottom and bottom to top and line also parallel to the Y-axis is called Vertical Line.
A vertical line is a line on the coordinate plane, where all points on the plane have the same x-coordinate.
Any point in this line will have same value for the x-coordinate.
Example: (3, 0), (5, 0) (-6, 0) etc. are the points of vertical lines.
We can understand this by the vertical lines mapped on a coordinate plane.
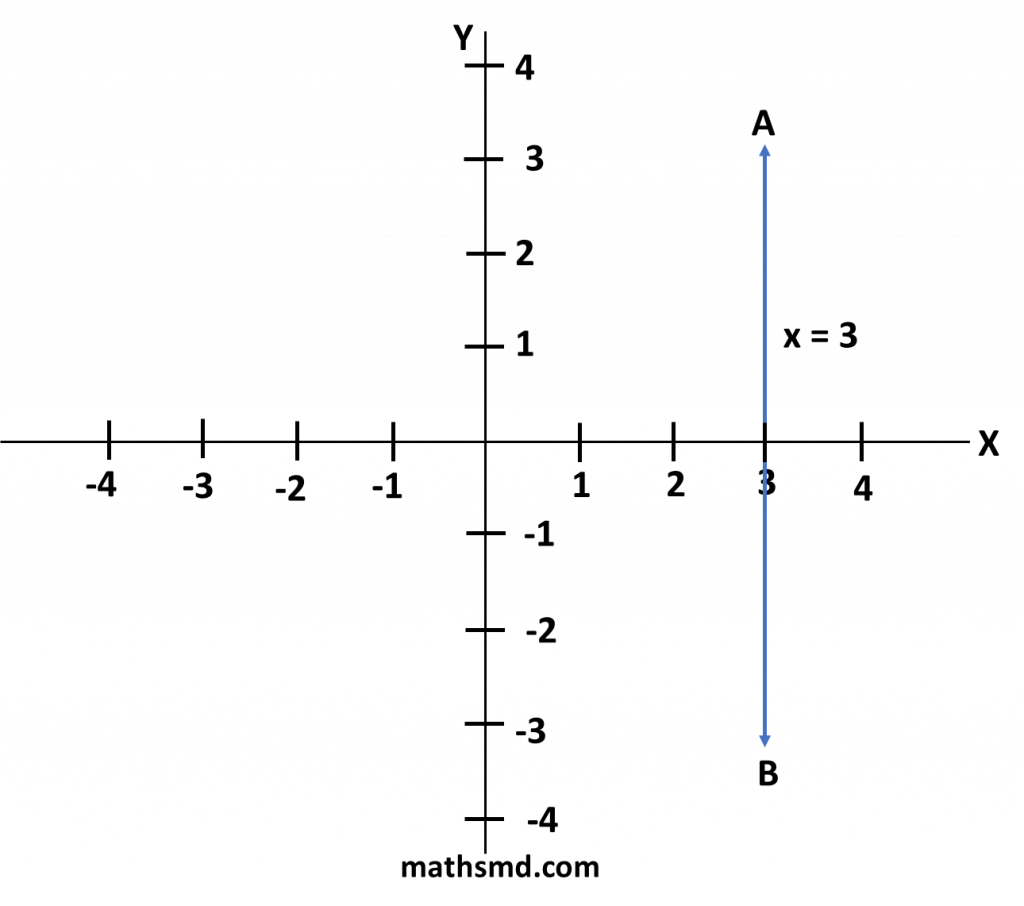
Plot the graph for the (i) x = 3 and (ii) x = -2.
(i) x = 3
x = 3 is a vertical line, that passes through x-axis, at a distance of 3 units on the right of the origin and is parallel to y-axis.
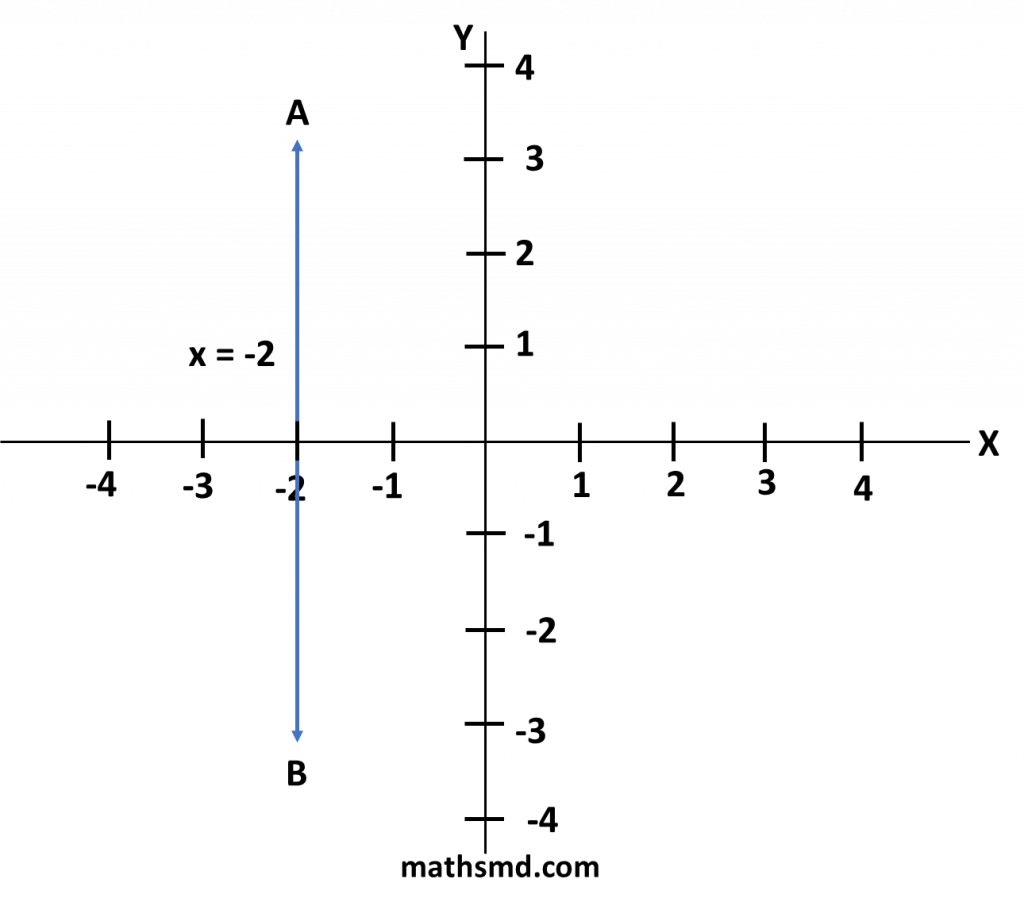
(ii) x = -2 is a vertical line, that passes through x-axis, at a distance of 2 units on the left of the origin and is parallel to y-axis.
Equation of Vertical Line
The equation of a vertical line in the graph is x = a. where x is the coordinate of any point on the line and a is where the line crosses the x-axis.

Properties of Vertical lines
(i) The vertical line is parallel to y-axis coordinate plane.
(ii) A vertical line is always perpendicular to the horizontal line.
Note that the equation is independent of y and any point on the vertical line satisfies the equation.
(iii) A vertical line has no slope or its slope is undefined or infinity as it has no y-intercept and the denominator in the slope formula is zero.