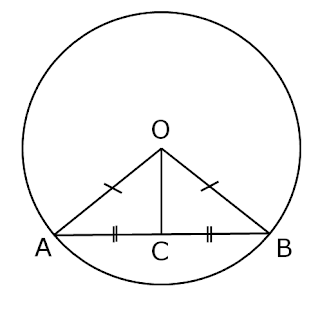
Theorem – The line drawn through the center of a circle to bisect a chord is perpendicular to the chord
The line drawn through the center of a circle to bisect a chord is perpendicular to the chord.
Given: A circle with center O, AB is chord of a circle and OC bisect chord at C. i,e. AC = CB.
To prove: OC ⊥ AB
Construction: join OA and OB.
Proof: In △ OCA and △ OCB
OA = OB (Radius of circle)
OC = OC (Common side)
AC = CB (Given)
Hence, △OCA ≅ △OCB (SSS Congruence rule)
∴ ∠OCA = ∠OCB …(1) (Corresponding parts of congruent triangles)
In line AB, ∠OCA and ∠OCB from linear pair
∴ ∠OCA + ∠OCB = 1800
From (1)
∴ ∠OCA + ∠OCA = 1800
∴ 2∠OCA = 1800
∴ ∠OCA = 180/2
∴ ∠OCA = 900
Thus, OC ⊥ AB
Hence proved