Algebraic Fractions – Multiplication

Multiplying Algebraic Fractions

How to Multiply Fractions?

When multiplying fractions, multiply the numerators(top numbers) with denominators(bottom numbers).

Multiplication of fractions is not like as the addition and subtraction of fractions.

When we solve the addition and subtraction of fractions the denominators should be same, but in any two fractions with different denominators are easily multiplied.

Multiplication of Algebraic Fractions

When we multiply any two algebraic fractions then the top numbers of the fractions(numerators) and the bottom numbers of the fractions(denominators) are multiplied together.

Example: p/2 x 3/q

= (p x 3)/(2 x q)

= 2p/3q

If a/b and c/d are two fractions, then the multiplication of a/b and c/d will be (a/b) x (c/d) = (a x c)/(b x d) = (ac)/(bd)

Where b and d are not equal to zero.

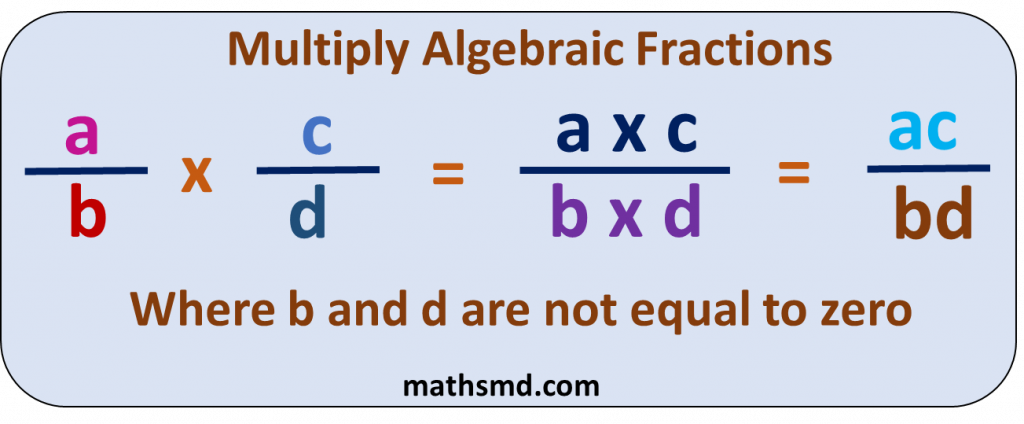
Let us see an example of multiplication of two fractions in steps.

Step 1: Multiply the numerators.

Step 2: Multiply the denominators.

Step 3: Simplify the fraction to its lowest form if possible.

Example: Multiply the fractions m/5 x 5/3m

We start from multiplying the numerators; m x 5 = 5m

Now multiply denominators; 5 x 3m = 15m

= (m x 5)/(5 x 3m)

=5m/15m

Now simplify this value in its lowest form.

The greatest common factor of 5 and 15 is 5, so to simplify the fraction 5/15, divide both 5 and 15, by 5.

Therefore, 5m/15m

= [(m x 5)/(5 x 3m)

= 1/3

Multiplying fractions with same denominator

Fractions that have same denominators are known as like fractions. Addition and subtraction of like fractions and unlike fractions are different.

The method of Multiplication of fractions with same denominator is same as multiplication of two fractions.

Here are steps given below.

First multiply the numerators, then multiply the denominators, and then fraction is reduced in its lowest form.

Let us understand this with an example;

3p/2 x 5/2

Step 1: Multiply the numerators, 3p x 5 = 15p

Step2 : Multiply denominators, 2 x 2 = 4

Step 3: The product of numerators and denominators is 15p/4, which cannot be reduced. Therefore answer is 15p/4.

Fractions With Different Denominators

Multiplying fractions with different Denominators is same as multiplication of like fractions.

Let us understand this with an example.

4/3 x 7m/5

Step 1: Multiply the numerators, 4 x 7m = 28m

Step2 : Multiply denominators, 3 x 5 = 15

Step 3: The product of numerators and denominators is 28m/15, which cannot be reduced. Therefore answer is 28/15

Example: Multiply the fractions a/6 x 3/5

We start from multiplying the numerators; 1 x 3 = 3a

Now multiply denominators; 6 x 5 = 30

= (1 x 3a)/(6 x 5)

= 3a/30

Now simplify this value in its lowest form.

The greatest common factor of 3 and 30 is 3, so to simplify the fraction 3a/30, divide both 3 and 30, by 3.

Therefore, 3a/30

= [(3 x a)/(3 x 10)

= a/10

Example: Multiply the fractions a/5 x 15/a

multiplying the numerators; a x 15 = 15a

multiply denominators; 5 x a = 5a

= (15 x a)/(5 x a)

= 15a/5a

Now simplify this value in its lowest form.

The greatest common factor of 15 and 5 is 5, so to simplify the fraction 15/5 divide both 15 and 5, by 5.

Therefore, 15a/5a

= [(a x 15)/(5 x a)]

= 3/1