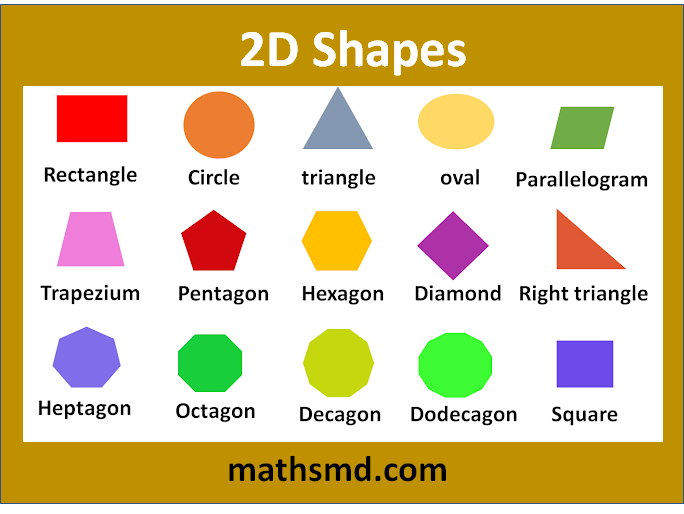
2D – Two Dimensional Shapes – Name -Definition – Properties – Geometry
2D – Shapes – Definition – Properties
Here is a detailed explanation of common 2D shapes, including their definitions, examples, diagrams, and properties:
Definition:
2D shapes are flat and also known as plane shapes, ‘2D’ stands for 2-dimensional. These shapes can be drawn on paper and have length and width. We can measure length and width.
Example: Rectangle, triangle, square, circle, oval, etc. are 2 dimensional objects.
1. Circle
Definition: A circle is a shape with all points the same distance from its center.
Example: Coins, plates, and wheels.
Diagram:

Properties:
- All points on the circle are equidistant from the center.
- The distance from the center to any point on the circle is called the radius.
- The longest distance across the circle (through the center) is called the diameter (d = 2r).
- The circumference (perimeter) is given by C = 2πr.
- The area is given by A = πr2.
2. Square
Definition: A square is a quadrilateral with all four sides of equal length and all four angles equal to 90 degrees.
Example: Chessboard squares, tiles, and crackers.
Diagram:

Properties:
- Sides: All four sides are equal in length.
- Angles: All four angles are right angles (90 degrees).
- Perimeter (P): The total length around the square.
- P = 4s (where sss is the length of a side).
- Area (A): The space enclosed by the square. A = s2.
3. Rectangle
Definition: A rectangle is a quadrilateral with opposite sides equal in length and all four angles equal to 90 degrees.
Example: Books, doors, and screens.
Diagram:

Properties:
- Sides: Opposite sides are equal in length.
- Angles: All four angles are right angles (90 degrees).
- Perimeter (P): The total length around the rectangle. P = 2l + 2w (where l is the length and w is the width).
- Area (A): The space enclosed by the rectangle. A = lw.
4. Triangle
Definition: A triangle is a polygon with three edges and three vertices.
Example: Traffic signs, pyramids (base), and slice of pizza.
Diagram:
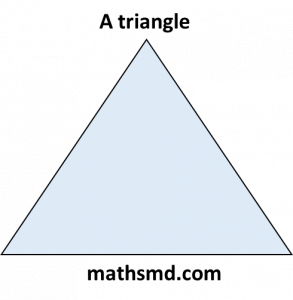
Properties:
- Types by Sides:
- Equilateral: All three sides are equal.
- Isosceles: Two sides are equal.
- Scalene: All three sides are different.
- Types by Angles:
- Acute: All angles are less than 90 degrees.
- Right: One angle is exactly 90 degrees.
- Obtuse: One angle is more than 90 degrees.
- Perimeter (P): The total length around the triangle. P = a + b + c (where a, b, and c are the lengths of the sides).
- Area (A): The space enclosed by the triangle. A = 1/2 × base × height.
5. Parallelogram
Definition: A parallelogram is a quadrilateral with opposite sides parallel and equal in length.
Example: Rhombus, diamond shapes, and certain desk tops.
Diagram:

Properties:
- Sides: Opposite sides are equal and parallel.
- Angles: Opposite angles are equal. Adjacent angles add up to 180 degrees.
- Perimeter (P): The total length around the parallelogram. P = 2a + 2b (where a and b are the lengths of the sides).
- Area (A): The space enclosed by the parallelogram. A = base × height.
6. Rhombus
Definition: A rhombus is a quadrilateral with all four sides of equal length and opposite sides parallel.
Example: Kite shapes, diamond-shaped road signs.
Diagram:

Properties:
- Sides: All four sides are equal in length.
- Angles: Opposite angles are equal. Adjacent angles add up to 180 degrees.
- Perimeter (P): The total length around the rhombus. P = 4s (where s is the length of a side).
- Area (A): The space enclosed by the rhombus. A = 1/2 × d1 × d2 (where d1 and d2 are the lengths of the diagonals).
7. Trapezoid (Trapezium in UK)
Definition: A trapezoid is a quadrilateral with at least one pair of parallel sides.
Example: Trapezoidal roof, handbags, and certain tables.
Diagram:
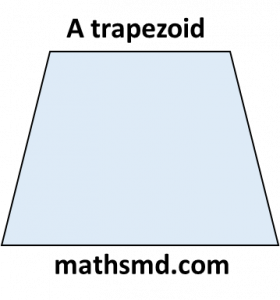
Properties:
- Sides: One pair of opposite sides are parallel (called bases), and the other pair are non-parallel (called legs).
- Angles: The angles on the same side of a leg are supplementary (add up to 180 degrees).
- Perimeter (P): The total length around the trapezoid. P = a + b + c + d (where a, b, c, and d are the lengths of the sides).
- Area (A): The space enclosed by the trapezoid. A = 1/2 × (b2 + b2) × h (where b1 and b2 are the lengths of the parallel sides, and h is the height).
These diagrams and explanations should help in understanding the basic properties of common 2D shapes.
