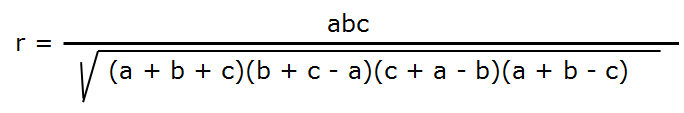Circumscribes and Inscribed Circles

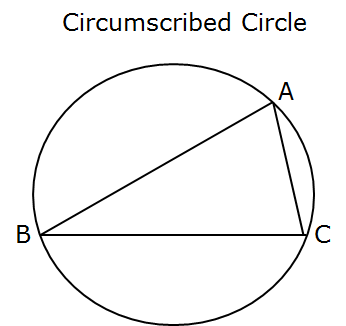
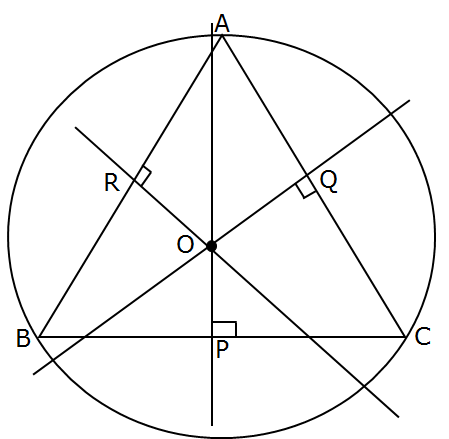
Circumscribed Circle

The circumscribed circle is one and only one circle that always passes through all three vertices (corners) of the triangle. 

The center of the circumscribed circle is a point where all the three perpendicular bisectors of the triangles sides are meet.

The center of the circumscribed circle is known as
circumcenter of the triangle.

The radius of the circumcircle is known as
circumradius of the triangle and is denoted by R.

The a method for constructing the circle that circumscribes a triangle.


Step 1: Draw a triangle.

Step 2: Draw the perpendicular bisector to each side of the triangle. Draw the lines long enough so that we see a point of intersection of all three lines.

Step 3: Draw the circle with radius at the intersection point of the bisectors that passes through one of the vertices. We should see that this circle passes through all three vertices and that is the desired circle.

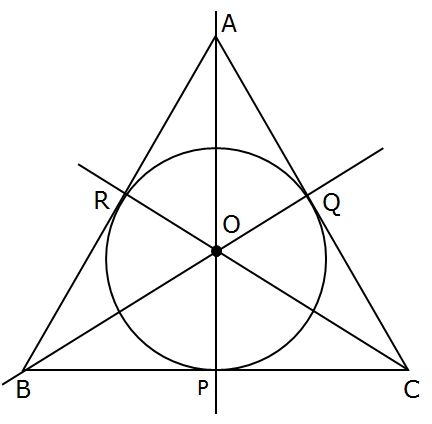
Inscribed Circle

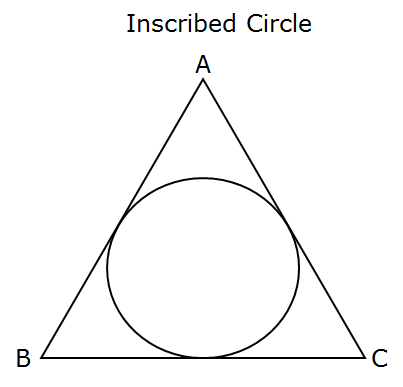
In a triangle, an inscribed circle is the largest circle that passes through all three sides of the triangle. 

The inscribed circle will touch each of the three sides of the triangle in exactly one point.

The center of the circle inscribed in a triangle the point, where the angle bisectors of the triangle meet is the incenter of the triangle.

The a method for constructing the circle that inscribes a triangle.


Step 1: Draw a triangle.

Step 2: Draw the angle bisector for each angle of the triangle. Draw the lines long enough so that we see a point of intersection of all three lines.

Step 3: Draw a line perpendicular to any side that passes through the intersection point. Mark the point on the side through which this line passes.

Step 4: Draw the circle with radius at the intersection point that passes through the point and this is the desired circle.

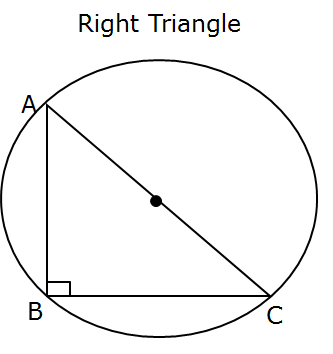
Right triangles

For a right triangle, the hypotenuse is a diameter of the circumcircle, and its center is exactly at the midpoint of the hypotenuse.

Equilateral triangle

For a equilateral triangle, where all three sides(a, b,c) are equal, the radius of the circumcircle is given by the formula:

r = s/√3 

Where s is the length of a side of the triangle.

One side and its opposite angle

If we know one side and its opposite angle, the diameter of the cirumcircle is given by the formula:

Diameter = a/SinA

where a is the length of one side, and A is the angle opposite that side of the triangle.

All three sides

If we know the length of all three sides(a,b,c) of a triangle, the radius of the circumcircle is given by the formula: