Rational and Irrational numbers

Usually most students feel difficult to understand the difference between rational and irrational numbers with the help of their definitions.

First we know about the terms that are useful to understand the concept of rational and irrational numbers.


1. Perfect square: 

If we multiply an integer with itself or same integer, we get a perfect square.

Example: 4, 9, 16, 25, 36, 49, 64, 100, 121 are perfect squares of numbers 2, 3, 4, 5, 6, 7, 8, 10, and 11 respectively.

Square roots of these perfect squares are 2, 3, 4, 5, 6, 7, 8, 10, and 11 respectively and all are integers.

2. Surds:

Surds are irrational numbers which are not squares of any integers also these are not multiples of an integer with itself.


3. Termainating decimal: 


Terminating decimals have finite number of digits

after the decimal point. 

Example: 2.51, 3.62, 7.24 have finite number of digits after the decimal point.

4. Non-Terminating decimal 

Non-Terminating decimals have infinite number of digits after the decimal point.

Example: √2 = 1.41423….

𝛑 = 3.142857……

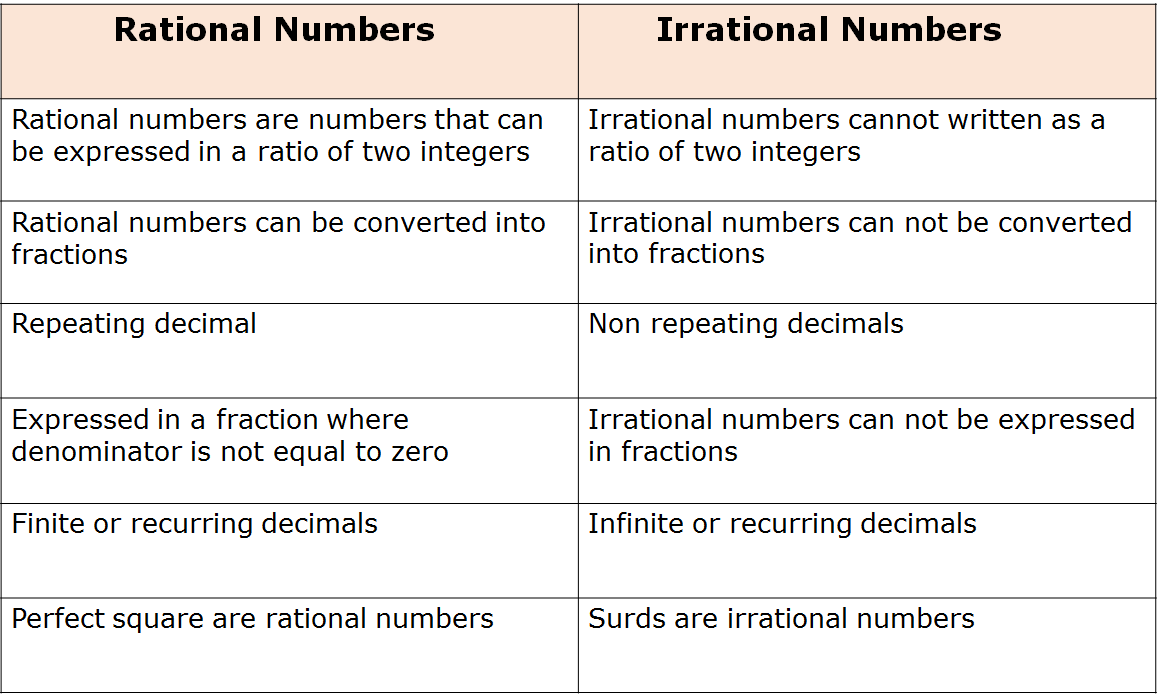
Here we learn, difference between rational and irrational numbers in brief.

What is a Rational Number?

A rational number is a expressed as a ratio of two integers, where denominator of the number should not be equal to zero.

Rational Numbers

Example: 

1. 3/2 is a rational number because numerator of the number is a integer that is 3 and denominator of the number is integer 2.

2. 5.1, 3.62, 7.24 have limited number of digits after the decimal point. So, all are rational numbers.

3. 25 is a rational number because it is a perfect square. 

4. 19/3 = 6.3333333…it means 19/3 is a repeating decimal. We know that repeating decimal is also a rational number.

5. 5/4 = 1.25,  5/4 is a rational numbers because the number of digits after decimal point is limited.

Now we can easily understand about irrational numbers.

 

What is a Irrational Number?

Irrational Numbers

Irrational numbers cannot be expressed in the form of fractions but it can be written as a decimal.

Irrational numbers cannot be expressed in the form of fractions but it can be written as a decimal.

An irrational number has infinite non-repeating number of digits after decimal point.

Example: 

1. A famous mathematical value 𝛑 (pi). 
The value of 𝛑 = 3.142857…

𝛑 has infinite non-repeating number of digits after decimal point, so 𝛑 is a irrational number.

2. √2 = 1.144213….

Similarly, √2 has infinite non-repeating number of digits after decimal point, so 𝛑 is a irrational number.

3. √7 is not an irrational number because it is a surd.

4. √2, √5, √7, √3, are surds.

When we find the square root of these surds we get,

√2 = 1.41…

√5 = 2.2360…

√3 = 1.73…

√7 = 2.64…

these are not integers.

To understand the difference between rational and irrational numbers, we look some numbers and try to separate them into rational and irrational numbers.

3/2,  0/9, √5, 3.26262626….., 2.333333….

1. 3/2 is a rational number because it can be expressed as a fraction. 

2. 0/9 is a rational number because it can be expressed as a ratio of two integers, where denominator of the number 0/9 is not be equal to zero.

3. √5 = 2.2360…. go to infinite.

√5 is a irrational number because it can not be written as a fraction.

4. 3.26262626…..

Here, number 26 is infinitely repeating pattern after decimal point. We know that repeating pattern after decimal point is also a rational number.

5. 2.3333333…….it means 2.33333… is a repeating decimal. We know that repeating decimal is also a rational number.

Conclusion:

At the end, we conclude that if a number is denoted in the form of a perfect square, terminating decimal, or repeating decimal, it means that it is a rational number. 

On other hand, if a number is denoted in the form of a surd or non-repeating decimal, it means that it is an irrational number. 

Rational numbers = Repeating decimals 
or 
Terminating decimals 
or 
perfect squares

Irrational numbers = Non-repeating decimals or surds