Divisibility Rule For 11 With Examples

Divisibility Rule for 11

A number is divisible by 11 if the difference between the sum of its digits in odd positions and the sum of its digits in even positions is either 0 or a multiple of 11.

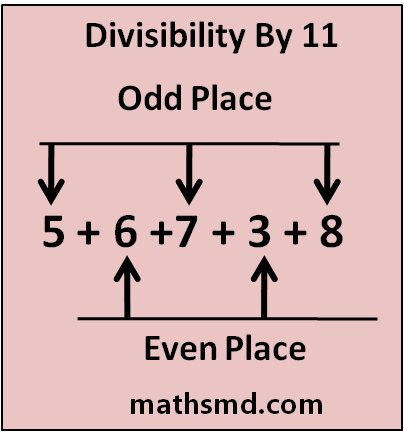
In above example

sum of even numbers 6 + 3 = 9

sum of odd numbers 5 + 7 + 8 = 20

Difference of numbers = 9 – 20 = -11

-11 is divisible by 11, so the number 56738 is divisible by 11.

Steps to Check Divisibility by 11

1. Identify the Positions: Label the digits of the number from right to left, starting with 1 (the rightmost digit is in position 1).
2. Separate Odd and Even Position Sums:

• Add the digits in odd positions.
• Add the digits in even positions.

1. Calculate the Difference: Subtract the sum of the even-positioned digits from the sum of the odd-positioned digits.
2. Check the Result: If the result is 0 or a multiple of 11, the original number is divisible by 11.

Examples

Example 1: 2728

1. Identify Positions:

• Digits: 2 (1st), 7 (2nd), 2 (3rd), 8 (4th)

1. Separate Sums:

• Odd positions: (2 + 2 = 4)
• Even positions: (7 + 8 = 15)

1. Calculate the Difference:

• Difference: (4 – 15 = -11)

1. Check the Result:

• (-11) is a multiple of 11.
• Conclusion: 2728 is divisible by 11.

---

Example 2: 123456

1. Identify Positions:

• Digits: 1 (1st), 2 (2nd), 3 (3rd), 4 (4th), 5 (5th), 6 (6th)

1. Separate Sums:

• Odd positions: (1 + 3 + 5 = 9)
• Even positions: (2 + 4 + 6 = 12)

1. Calculate the Difference:

• Difference: (9 – 12 = -3)

1. Check the Result:

• (-3) is not a multiple of 11.
• Conclusion: 123456 is not divisible by 11.

---

Example 3: 121

1. Identify Positions:

• Digits: 1 (1st), 2 (2nd), 1 (3rd)

1. Separate Sums:

• Odd positions: (1 + 1 = 2)
• Even positions: (2)

1. Calculate the Difference:

• Difference: (2 – 2 = 0)

1. Check the Result:

• 0 is a multiple of 11.
• Conclusion: 121 is divisible by 11.

---

Example 4: 987654

1. Identify Positions:

• Digits: 9 (1st), 8 (2nd), 7 (3rd), 6 (4th), 5 (5th), 4 (6th)

1. Separate Sums:

• Odd positions: (9 + 7 + 5 = 21)
• Even positions: (8 + 6 + 4 = 18)

1. Calculate the Difference:

• Difference: (21 – 18 = 3)

1. Check the Result:

• 3 is not a multiple of 11.
• Conclusion: 987654 is not divisible by 11.

---

Example 5: 484

1. Identify Positions:

• Digits: 4 (1st), 8 (2nd), 4 (3rd)

1. Separate Sums:

• Odd positions: (4 + 4 = 8)
• Even positions: (8)

1. Calculate the Difference:

• Difference: (8 – 8 = 0)

1. Check the Result:

• 0 is a multiple of 11.
• Conclusion: 484 is divisible by 11.

Summary

To determine if a number is divisible by 11:

• Separate the digits into odd and even positions.
• Calculate the sums for both positions.
• Find the difference and check if it’s 0 or a multiple of 11.

This method is efficient and helps quickly check for divisibility by 11 without performing long division.