Closure Property of Rational Numbers

What are Rational Numbers?

Rational numbers are numbers which can be represented in the form of p/q, where p and q are any two integers and q is not equal to zero(q ≠ 0).

Closure Property of Rational Numbers

When we perform any operation on a rational number, such that the resultant also be a rational number, then we say it follows closure property of rational numbers over that operation.

So, if any operation of two rational numbers satisfies the above mentioned property we say it is closed under that particular operation.

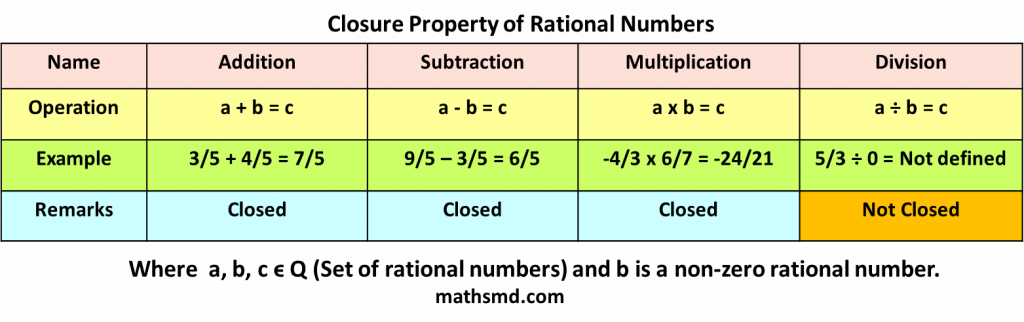
Closure property of rational numbers states that when any two rational numbers are added, subtracted or multiplied the result of all three cases will also be a rational number.

Let know about how the closure property of rational numbers works on all the basic arithmetic operations. We will understand this property on each operation using various examples.

Closure Property of addition

Closure property of addition of rational numbers states that the sum of two rational numbers is also a rational number.

If a and b are rational numbers then, a + b is also a rational number.

Example: Let us take two rational numbers 1/4 and 1/5

1/4 + 1/5

= (5 + 4)/20

= 9/20

Sum of two rational numbers 1/4 and 1/5 is also a rational number.

We can say that the rational numbers are closed under addition.

Closure Property of Subtraction

Closure property of subtraction of rational numbers states that the difference of two rational numbers is also a rational number, i.e.,

if a and b are rational numbers then, a – b is also a rational number.

Example: 1/5 – 1/4

= (4 – 5)/20

= -1/20

Subtraction of two rational numbers 1/4 and 1/5 is also a rational number.

We can say that the rational numbers are closed under subtraction.

Closure Property of multiplication

The closure property of multiplication of rational numbers states that when any two rational numbers are multiplied the result will also be a rational number.

For any two rational numbers a and b, a x b is also a rational number.

Example: Let us take two rational numbers 1/5 and 1/3

Example: 1/5 x 1/3

= (1 x 1)/(5 x 3)

Here result is 1/15, which is also a rational number.

multiplication of two rational numbers 1/4 and 1/5 is also a rational number.

We can say that the rational numbers are closed under multiplication.

Closure Property of Division

Example: 1/5 ÷ 1/3

= 1/5 x 3/1

Here result is 3/5, which is also a rational number.

For any rational number a, a ÷ 0 is not defined.

For example rational number 9, 9 ÷ 0 is not defined.

We find that closure property is not applicable for division as division by zero(0) is not defined.

So, we can say that closure property is applicable for division, if we exclude zero, then rational numbers are closed under division.

Note: When any two rational numbers are added, subtracted or multiplied the result of all three cases will also be a rational number.