Triangle – Definition and Properties

The origin of term “Triangle” from latin word tri (“Three”) and angulus means (“angles”).

A “Triangle” is a simple closed curve or a three sided polygon.

A triangle has three angles and three sides and three vertices. It is one of the basic shape in geometry.  

In Euclidean geometry any non-collinear, three points, determine a unique triangle. 

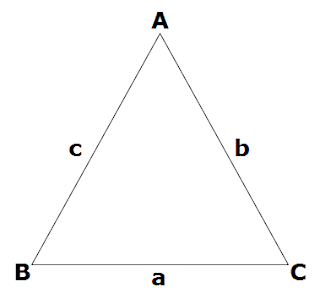
The triangle with three vertices A, B and C ABC is denoted by “△ ABC”. 

Three “Sides” of triangle are AB, BC, and CA. 

Three “Vertices” of triangle are A, B and C.

Three “Angles” of triangle are ∠A, ∠B and ∠C.

∠ABC, ∠BCA and ∠CAB are interior angles of △ABC.

The total of “Interior angles” of a triangle, ∠ABC, ∠BCA and ∠CAB. is always 180⁰.

“Perimeter” – The sum of it’s three sides are AB, BC, and CA (AB+BC+CA), or the distance around the triangle is known as the perimeter.

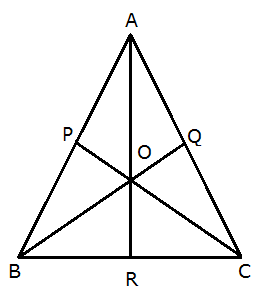
“Median”- A line from a vertex to the midpoint of the opposite side is known as the median of triangle.

A triangle has three medians, in △ABC, three medians are AR, BQ and PC  

“Centroid”- The three medians are intersect to each other at a single point, called the “Centroid” of the triangle. In △ABC, O is the “Centroid”.

Note- When show a specifying angle, the vertex is always written as the middle letter.

  Properties of Triangles

These are some important properties of triangles.

1. The total of all interior angles is always 180⁰. 
This is called the angle-sum property.

2. The sum of the lengths of any two sides of a triangle is greater than the length of the third side.

3. In the same way, the difference between the length of any two sides of a triangle is less than the length of the third side.

4. The side opposite the the largest angle, is the longest side of the triangle.

In above figure, ∠Y is the largest angle of  the triangle XYZ and the and opposite side of angle Y (hypotenuse), is the largest side of the triangle and the side opposite to the smallest angle, is the shortest side of the triangle.

5. Formula for Area of the triangle = 1/2 (base x height).

6. A line from a vertex to the midpoint of the opposite side is known as the median of triangle.

In above triangle ABC, AR is the median taking mid point of BC as R, CP is also median, as P is mid point of AB, and Q is mid point of AC, so BQ is median. 

Thus, these three AR, CP and BQ are the medians of the triangle.

The three medians of the triangle are intersect to each other at a single point, called the “Centroid” of the triangle.

In △ABC, O is the “Centroid” of the triangle.

7. The altitude has one endpoint at a vertex of the triangle and other on the line containing the opposite side. 

The altitudes of the triangle are concurrent and their point of concurrence is called the orthocentre of the triangle. 

8. In the figure above, ∠A is the largest angle and the side opposite to it, BC is the largest side of the triangle.

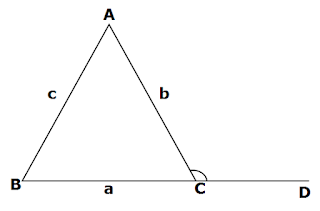
The measure of a exterior angle of a triangle is equal to sum of its interior opposite angles.

This is called the exterior angle property of a triangle.

Here, ∠ACD is the exterior angle of the triangle ABC.

∴ ∠ACD = ∠ABC + ∠CAB (exterior angle property).

9. Usually the name of each vertex of a triangle with a single capital letter (upper-case) like A, X, B, Y, etc.

The name of sides can be with a single small letter (lower case) like a, b, x, y, etc and named after the opposite angle.

So, in the given figure we can see that side a is opposite vertex A, side b opposite vertex B and side c is opposite vertex C.

The side of a triangle is a line segment joining two vertices.

So, the side a, would be called BC side b, would be called AC and side c, would be called AB.

Solved questions:

Q1. In a triangle ABC, ∠A = ∠B = 45⁰ then the name of triangle is

a. equilateral angled triangle

b. acute angled triangle 

c. obtuse angled triangle

d. right angled triangle

Solution: In △ABC, 

Sum of all interior angles is 180^0.

∴ ∠A + ∠B  + ∠C = 180⁰

 ∴ 45⁰ + 45⁰ + ∠C = 180⁰

 ∴ 90⁰ + ∠C = 180⁰

  ∴ ∠C = 180⁰ – 90⁰

  ∴ ∠C = 90⁰

∴ It is a right angled triangle.