Intersection of sets 

Definition:

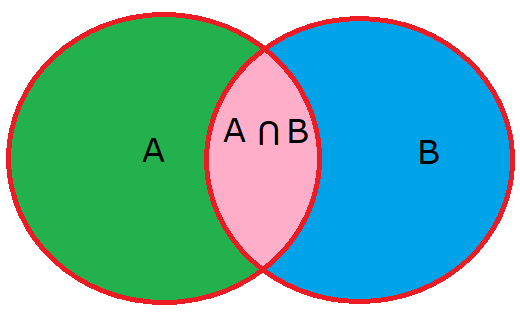
The ‘Intersection of two sets’ A and B is the set of all elements, which belong to both A and B.

or simply, 

The ‘Intersection of two sets’ A and B is the set of all elements, which are common in both A and B.

Symbol  ‘∩’ is used to denoted the Intersection of two sets A and B and read as ‘A intersection B’

we write as A∩B = {X : X ∈ A and X : ∈ B}

Example: Let A = {1, 2, 3, 4, 5,}  and B = {3, 5, 1, 7, 8}

     A∩B = elements, which are common in both A and B

A∩B = {1, 2, 3, 4, 5}∩{3, 5, 1, 7, 8}

                            ∴ A∩B = {1, 3, 5}

         answer:    A∩B = {1, 3, 5}

Representing the intersection of sets in a Venn diagram

Venn Diagram

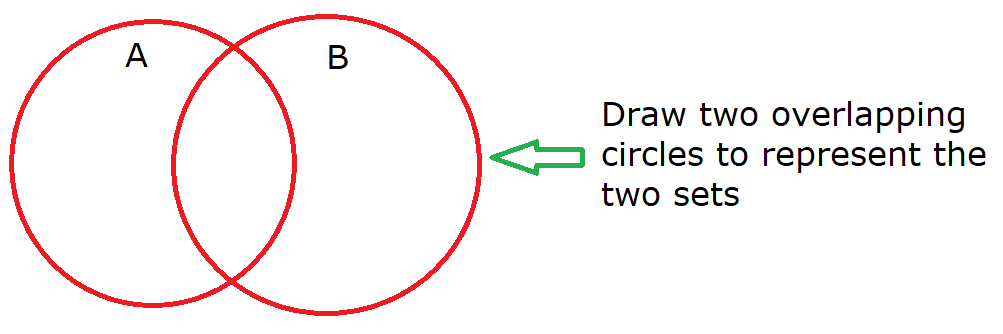
The venn diagram below shows the intersection of two sets

A = {1, 2, 3, 4, 5, 6}, and B = {1, 2, 3, 7, 8, 9}

Step 1: Draw two overlapping circles to represent the two sets.

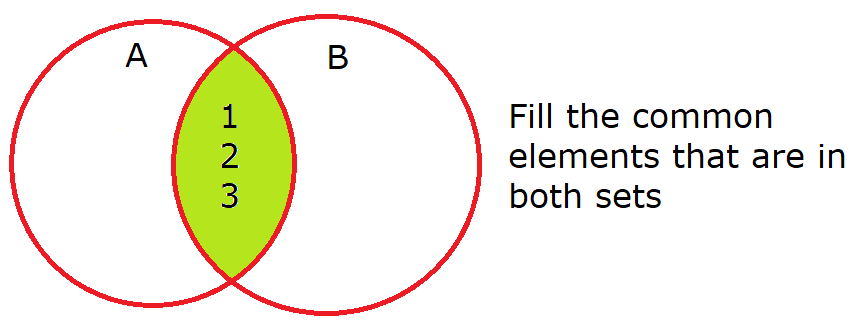
Step 2: Here {1, 2, 3} are (common elements) lie in both sets, so we place them in the overlapping region of two circles.

Step 3: The remaining elements of A are {4, 5 and 6}, these are placed inside A, but outside B.

The remaining elements of B are {7, 8 and 9}, these are placed inside B, but outside A.

Thus, the overlapping region represents A∩B = {1, 2, 3}.

Example: Let A = {1, 2, 3, 4,}  and  B = {3, 4, 5, 6,}

Now we will draw a Venn diagram of two overlapping circles.

The middle part of the circles (overlapping region) represents the common elements in both sets.

Common elements in both sets are {3, 4}

Left circle represents set A and right circle represent set Y. The shades region in the middle represents common elements in set A and set B.

That is their intersection. The intersection of A and B is (3, 4).

The Venn diagram is easy to see that the elements (3, 4) are common in both sets. So the intersection of set A and set B is (3, 4)is written as

∴ A∩B = {3, 4}

Example: Let X = {p, q, r} and Y = {l, m, n}

Then, X∩Y = {p, q, r}∩{l, m, n}

∴ X∩Y = ∅

Example: Let X = {p, q, r} and Y = {r, q, p}

Then, X∩Y = {p, q, r}∩{r, q, p}

∴ X∩Y = {p, q, r}

Note: Here X = Y = X∩Y

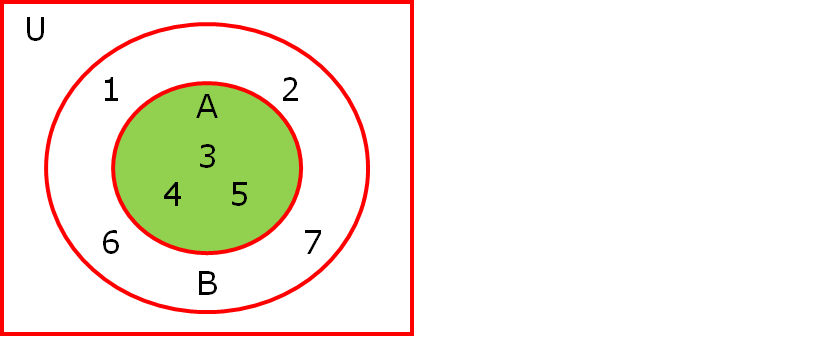
Representing subsets on Venn diagram

If a set A is a subset of set B, then we place the circle representing set A is drawn inside the circle representing set B.

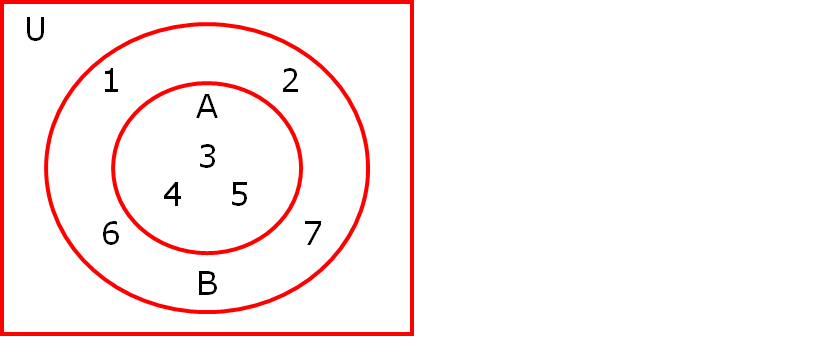
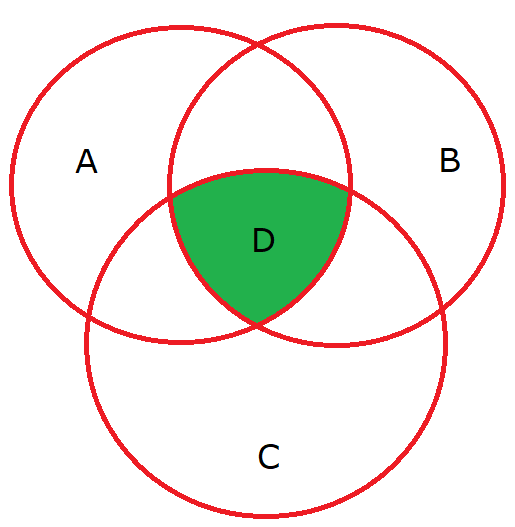
The shaded region is A∩B∩C

        Properties of Operation of Intersection

1. A∩B = B∩A (Commutative Law)

2. (A∩B)∩C = A∩(B∩C) (Associative Law)

3. ∅∩A = ∅ (Law of A and ∅)

4. A∩A = A (Idempotent Law) 

5. A∩(B∪C) = (A∩B)∪(A∩C)(Distributive Law)

UA = A

1. A∩B = B∩A (Commutative Law)

Suppose A = {a, b, c, d} and B = {a, b, e, f}

A ∩ B = {a, b}

B ∩ A = {a, b}

∴ A ∩ B = B ∩ A

2. (A∩B)∩C = A∩(B∩C) (Associative Law)

Suppose A = {a, b, c, d} and B = {a, b, c, e, f}, and C = {r, s, t, u, v, a, b , }

A ∩ B = {a, b, c}

(A∩B)∩C = {a, b, c} ∩ {r, s, t, u, v, a, b}

(A∩B)∩C = {a, b}

B ∩ C = {a, b}

A∩(B ∩ C) = {a, b,}

(A ∩ B)∩C = {a, b}

(A ∩ B)∩C = A∩(B ∩ C) = {a, b}

3. ∅∩A = ∅ (Law of A and ∅)

Suppose, A = {1, 2, 3}, and B = ∅

∴ A ∩ B = ∅

∴ ∅ ∩ A = ∅