Right Angle Triangle – Definition – Formula – Properties

What is a Right Angle Triangle?

A right angle triangle is a type of triangle. A right angle triangle plays an important role in trigonometry.

A triangle in which one of the interior angle is 90º or a right angle is a right triangle.

Right Triangle Definition:

When an angle of a triangle is 90º or right angle and the other two angles are acute angles, then the triangle, is called a right angle triangle or simply right triangle.

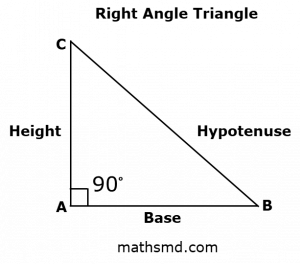
In above figure, triangle ABC is a right triangle, ∠BAC is a right angle, AB is the base of the triangle, AC is the height of the triangle and BC is the hypotenuse of the triangle.

The longest side of the right triangle, which is also the side opposite to the right angle, is the hypotenuse and other two sides of the right triangle are the height and the base.

Right Angle Triangle Formula

The great Greek philosopher, Pythagoras, invent an important formula for a right triangle, it was named after him as Pythagoras Theorem.

The formula states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

Right triangle formula can be represented as,

The square of the hypotenuse is equal to the sum of the square of the base and the square of the height.

(Hypotenuse)² = (Base)² + (Height)²

Right Angle Triangle Area.

The formula to find the area of a right triangle is given by

Area (A) = (1/2 x Base X Height) square units.

Height = Perpendicular

Right Angle Triangle Properties

Some important properties of a right triangle are listed below.

A right triangle has one angle is always 90 or right angle.

The side opposite angle of 90 is called the hypotenuse.

The sum of the other two interior angles is equal to 90.

The hypotenuse is always the longest side of the triangle.

The other two sides adjacent to the right angle are called base and perpendicular.

A right triangle cannot have any obtuse angle.

The angles other than right angle must be acute angles, (less than 90). the circumcircle of the right triangle passes through all three vertices and the radius of this circle is equal to half of the length of the hypotenuse.

Perimeter of a right triangle

Perimeter of a right triangle is the sum of the measures of all three sides.

It is the sum of base, height and hypotenuse of the right triangle.

In above figure, the perimeter of the right triangle is equal to the sum of the sides (AB + BC + AC)