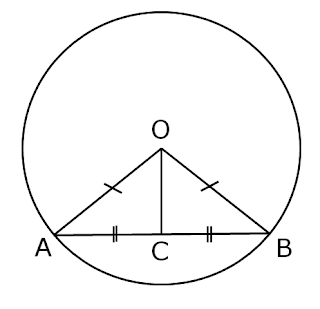
Theorem – The line drawn through the center of a circle to bisect a chord is perpendicular to the chord

The line drawn through the center of a circle to bisect a chord is perpendicular to the chord.

Given:  A circle with center O, AB is chord of a circle and OC bisect chord at C. i,e. AC = CB.

To prove: OC ⊥ AB

Construction: join OA and OB. 

Proof:  In △ OCA and △ OCB

OA = OB (Radius of circle)

OC = OC (Common side)

AC = CB  (Given)

Hence, △OCA ≅ △OCB (SSS Congruence rule)

∴ ∠OCA = ∠OCB …(1) (Corresponding parts of congruent triangles)

In line AB,  ∠OCA and ∠OCB from linear pair

∴ ∠OCA + ∠OCB = 1800

From (1)

∴ ∠OCA + ∠OCA = 1800

∴ 2∠OCA = 1800

∴ ∠OCA = 180/2

∴ ∠OCA = 900

 Thus, OC ⊥ AB 

                                         Hence proved

Related posts:

  1. Theorem – The perpendicular from the center of a circle to a chord bisects the chord
  2. Theorem – The perpendicular from the center of a circle to a chord bisects the chord
  3. Theorem – If the angles subtended by the chords of a circle at the centre are equal, then the chords are equal
  4. Theorem – If the diagonals of a Quadrilateral bisect each other then that Quadrilateral is a Parallelogram
  5. Radius of a Circle
  6. Cyclic Quadrilaterals: Definition, Properties, Examples
  7. Theorem – Equal chords of a circle subtend equal angles at the center
  8. In a parallelogram, opposite sides are equal
  9. What is a Vertex in geometry – Definition and Examples
  10. The tangent at any point of a circle is perpendicular to the radius through the point of contact

Leave a Reply

Your email address will not be published. Required fields are marked *