Problems with Solutions on Trigonometric Ratios
Solutions of Trigonometric Ratios
(1) If sin A = 4/5, find the other trigonometric ratios of the angle A.
Solution:
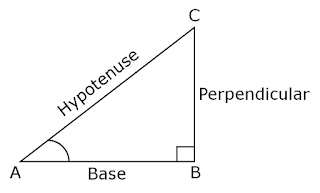
Let us draw a right △ ABC in which ∠B = 900
We know that, sin A = 4/5 = BC/AC
Therefore, if BC =4k, then AC = 5k, where k is a positive number.
Now, using the Pythagorean Theorem, we have
AC2 = AB2 + BC2
(5k)2 = AB2 + (4k)2
25k2 = AB2 + 16k2
25k2 – 16k2 = AB2
9k2 = AB2
So, AB = 3k
Now, we write all the trigonometric ratios using their definitions.
(1) Cosec A = AC/BC = 5k/4k = 5/4,
(2) Cos A = AB/AC = 3k/5k = 3/5,
(3) Sec A = AC/AB = 5k/3k = 5/3,
(4) Tan A = BC/AB = 4k/3k = 4/3,
(5) Cot A = AB/BC = 3k/4k = 3/4.
(2) If sec A = 13/12, find the other trigonometric ratios of the angle A.
Solution:
Let us draw a right △ ABC in which ∠B = 900
We know that, sec A = 13/12 = AC/AB
Therefore, if AC =13k, then AB = 12k, where k is a positive number.
Now, using the Pythagorean Theorem we have,
AC2 = AB2 + BC2
(13k)2 = (12k)2 + BC2
(13k)2 – (12k)2 = BC2
169k2 – 144k2 = BC2
25k2 = BC2
So, BC = 5k
Now, we write all the trigonometric ratios using their definitions.
(1) Cosec A = AC/BC = 13k/12k = 13/12,
(2) Cos A = AB/AC = 5k/13k = 5/13,
(3) Sec A = AC/AB = 13k/5k = 13/5,
(4) Tan A = BC/AB = 12k/5k = 12/5,
(5) Cot A = AB/BC = 5k/12k = 5/12.
(3) In △ ABC, right angle at B, AB = 7cm and AC – BC = 1 cm.
Find the value of sin C and cos C.
Solution: In △ ABC, using the Pythagorean Theorem, we have
AC2 = AB2 + BC2
AC – BC = 1
∴ AC = 1 + BC
(1 + BC)2 = AB2 + BC2
1 + BC2 + 2BC = AB2 + BC2
∴ 1 + BC2 + 2BC – BC2 = AB2
∴ 1 + 2BC = AB2
∴ 1 + 2BC = 72
∴ 1 + 2BC = 49
∴ 2BC = 49 – 1
∴ 2BC = 48
∴ BC = 48/2
∴ BC = 24 cm.
AC = 1 + BC
AC = 1 + 24
AC = 25cm.
Now,
AB = 7 cm, BC = 24 cm, and AC = 25cm.
Therefore, sin C = AB/AC
sin C = AB/AC = 7/25 cm,
cos C = BC/AC
cos C = BC/AC = 24/25 cm.
sin C = 7/25 and cos C = 24/25 cm.
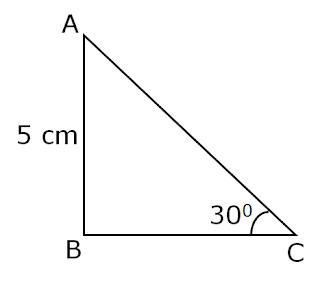
(4)In △ ABC right angled at B, AB = 5cm and
∠ACB = 300.
Find the lengths of the sides BC and AC.
Solution:
First we find the length of BC, so we will choose the trigonometric ratio between BC and AB.
Since BC is the base for angle C, and AB is the perpendicular for angle C.
Therefore, tan C = AB/BC
= 5/BC (AB = 5 cm)
tan 300 = 1/√3
∴ 1/√3 = 5/ BC
BC = 5√3 cm.
Now, for length of side AC we take,
sin 300 = AB/AC
sin 300 = 1/2
1/2 = 5/AC (AB = 5 cm)
AC = 5 x 2
i.e., AC = 10 cm.
(5) If tan A = 15/8, find the other trigonometric ratios of the angle A.
Solution:
Let us draw a right △ ABC in which ∠B = 900
We know that, tan A = 15/8 = BC/AB
Therefore, if BC =15k, then AB = 8k, where k is a positive number.
Now, using the Pythagorean Theorem, we have
AC2 = AB2 + BC2
AC2 =(8k)2+ (15k)2
AC2 = 64k2+ 225k2
AC2 = 289k2
AC2 = (17k)2
So, AC = 17k
Now, we write all the trigonometric ratios using their definitions.
(1) sin A = BC/AC = 15k/17k = 15/17,
(2) Cosec A = AC/BC = 17k/15k = 17/15,
(3) Cos A = AB/AC = 8k/17k = 8/17,
(4) Sec A = AC/AB = 17k/8k = 17/8,
(5) Cot A = AB/BC = 8k/15k = 8/15.
(6) In △ ABC right angled at B, if tan A = 1/√3, find the other trigonometric ratios of the angle A, and the value of
(i) sin A cosC + cos A sin C
(ii) cos A cosC – sin A sin C
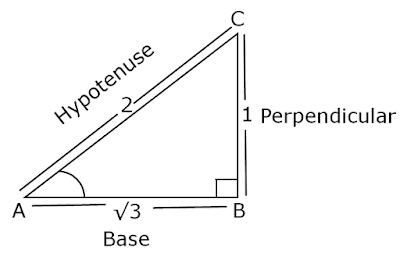
Solution: Let us draw a right △ ABC in which ∠B = 900
We know that, tan A = 1/√3
= BC/AB
BC/AB = 1/√3
Therefore, if BC = 1k and AB = √3k, where k is a positive number.
Now, using the Pythagorean Theorem, we have
AC2 = AB2 + BC2
AC2 =(√3k)2+ (1k)2
AC2 = 3k2 + k2
AC2 = 4k2
AC2 = (4k)2
So, AC = 2k
Now, we write all the trigonometric ratios using their definitions.
(1) sin A = BC/AC = k/2k = 1/2,
(2) Cosec A = AC/BC = 2k/k = 2/1,
(3) Cos A = AB/AC = √3k/2k = √3/2,
(4) Sec A = AC/AB = 2k/√3k = 2/√3,
(5) Cot A = AB/BC = √3k/1k = √3/1.
(6) sin C = AB/AC = √3k/2k = √3/2.
(7) Cos C = BC/AC = √k/2k = √1/2.
Now, we put the value in,
(i) sin A cosC + cos A sin C
= (1/2)(1/2) + (√3/2)(√3/2)
= 1/4 + 3/4
= 4/4
(i) sin A cosC + cos A sin C = 1.
(ii) cos A cosC – sin A sin C
= (√3/2)(1/2) – (√1/2)(√3/2)
= √3/4 – √3/4
= 0
(i) sin A cosC + cos A sin C = 1.
(ii) cos A cosC – sin A sin C = 0. Solution