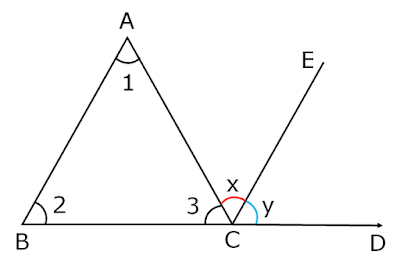
Exterior Angle of a Triangle

If any side of a triangle is extended then the exterior angle of triangle is equal to the sum of its interior opposite angles.

Given : A △ABC, side BC of △ABC is extended, 
∠ACD is an exterior angle.

To Prove : The sum of measure of exterior angle of triangle is equal to the sum of its interior opposite angles. so,

m∠ACD = m∠BAC + m∠ABC

Construction: Draw a line CE parallel to side BA through C.

Proof : BA ∥ CE and AC is a transversal.

Therefore,  ∠1 = ∠x ….(i)   (pair of alternate angles)

                BA ∥ CE and BD is a transversal.

Therefore,  ∠2 = ∠y ….(ii)  (pair of corresponding angles)

            add eq. (i) and (ii) we get

                         ∠1 + ∠2 = ∠x + ∠y 

          Now,        ∠x + ∠y = ∠ACD (From figure)

          Hence,     ∠1 + ∠2 = ∠ACD

                    ∠BAC + ∠ABC = ∠ACD

                    ∠ACD = ∠ABC + ∠BAC

We see that the exterior angle of triangle is equal to the sum of its interior opposite angles.

                                              Hence Proved.