Congruent triangles Worksheet

   Problems and Solutions

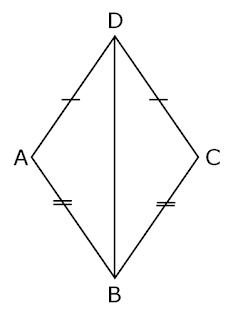
Example : (1) In figure if AD = CD and AB =  CB.

(i) Find the three pairs of equal parts in △ABD and 
△CBD.

(ii) Is △ABD ≅ CBD ? Why or why not?

(iii) Does BD bisect ∠ABC? give reason.

Solution : (i) In △ABD and △CBD, three pairs of equal parts are, Sides of triangles.

                        AD = CD (given) 

                        AB =  CB (given)

                 and BD = BD (Common in both triangles)

(ii)                △ ABD ≅  △ CBD 

        From solution (i), by (SSS congruence rule)

(iii)            BD bisect ∠ABC, because

                      ∠ABD = ∠CBD (Corresponding parts of congruent triangles)

Example : (2) Check whether two triangles are congruent or not.

Solution : In figure △ ABD and △ PQR are right angled triangles.

                     In △ ABC and △ PQR,

                 ∠ABC = ∠PQR (Both are right angles)

            side   BC = QR (Given)

 Hypotenuse  AC = PR (Given)

Hence,  △ ABC ≅   △ PQR (RHS congruence rule)

If the hypotenuse and one side of a right angled triangle are respectively, equal to the hypotenuse and one side of another right angled triangle, then the triangles are congruent.

Example : (3) Check whether two triangles are congruent or not.  

Solution : In figure △ ABD and △ PQR are right angled triangles.

                     In △ ABC and △ PQR,

                   ∠ABC = ∠PQR (Both are right angles)

              side   BC = QR = 4 cm (Given)

    Hypotenuse  AC = PR = 5 cm (Given)

         Hence,  △ ABC ≅ △ PQR (RHS congruence rule)

If the hypotenuse and one side of a right angled triangle are respectively equal, to the hypotenuse and one side of another right angled triangle, then the triangles are congruent.

Example : (4) Which congruence criterion do you use in the following.

                         Given AB = PQ                                  

BC = QR                          

and   AC = PR

Solution :  In figure △ ABC and △ PQR, given that
                          AB = PQ 

                                  BC = QR 

                          and   AC = PR

In △ABC and △PQR, three pairs of equal parts are, sides of triangles.

Hence,  △ ABC ≅ △ PQR (SSS congruence rule

Example : (5) Check whether two triangles are congruent or not.

Solution : In figure △ ABC and △ PQR, given that

                    AB = PQ (From the figure)

                    BC = QR (From the figure)

Given information for the congruence of two triangles, in the figure is not sufficient.

We can not conclude, whether the two △ ABC and △ PQR are congruent or not.

Example : (6) Check whether two triangles ABD and CDB are congruent or not.

Solution : Two triangles, △ ABD and △ CDB, are given.
In △ ABD and △ CDB,

                          AB = DC  (From figure)

                          BD = BD  (Common in both triangles)                       ∠ABD = ∠CDB (From figure)   

Hence,  △ ABD ≅ △ CDB (SRS congruence rule)

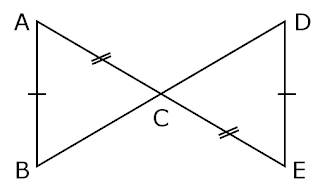
Example : (7) Check whether two triangles ABC and DEC are congruent or not. 

Solution : In the figure two triangles are △ ABC and △ DEC, and given that,                       AB = DE  (From figure)                                             AC = CE  (From figure) 
                   ∠ACB = ∠DCE (Vertically opposite angles)
From above three congruent parts of triangles, we get ASS congruence, but ASS congruence does not work for congruent triangles.
Hence, △ ABC and △ DEC are not congruent.  

Example : (8) Check whether two triangles AMP and AMQ are congruent or not. 

Solution : In the figure two triangles are △ APM and △ AQM, and given that,                       

PM = QM  (From figure)
                       AM = AM  (Common in both ) 
                      ∠AMP = ∠AMQ (Given)
   Hence,  △ AMP ≅ △ AMQ (SAS congruence rule)