Finite and Infinite Sets Definition – Examples – Properties

Definition:              

                           Finite Sets

If a set contains finite or limited or (countable) number of elements is called Finite Set.

Examples of finite sets:

Example: (i) The vowels in English alphabets.

A = {a, e, i, o, u,}

The set of players in a football team.    

              A = {x : x is players of a football team}

(ii) The set of four positive even numbers less than 10.

                        A = {2, 4, 6, 8}                 

                         A = {1, 2, 3,}

Here in both examples, set A have limited number of elements, so A is a finite set.

(iii) A set of all English alphabets, we can count the numbers of English alphabets so it is a finite set. 

A = {a, b, c, d, e, f, g, h, i, j, k, l, m, 
n, o, p, q, r, s, t, u, v, w, x, y, z}

In above example the cardinality of the set is 26, because the number of elements are 26.

So, n(A) = 26.

iv. Set of all natural numbers between 1 and 75.

N = {1, 2, 3, 4,…, 75}

N = 75

n(N) = 75

v. Set of all days in a week.

D = {Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, Saturday}

n(D) = 7

vi. Set of all colors of rainbow.

R = {Violet, Indigo, Blue, Green, Yellow, Orange, Red}

n(R) = 7

All the above examples are finite sets because the number of elements are countable in each set, and their cardinality is a natural number.

We observe that we can list all the elements of a set and write them in the curly braces or we can write in roster form are called the finite sets.

                Properties of finite sets

1.The union of two finite sets is finite.
2.The elements of a finite set is countable.
3.The power set of a finite set is finite.

                 Cardinality of a finite set

The cardinality of a set X is n(X) = a, where a represents the number of elements of set X.

In above example the cardinality of the set is 26, because the number of elements are 26.

So, n(A) = 26.

                  Is finite set a empty set?

First we need to understand the meaning of empty set then understand the answer of this question.

Empty Set – A set which does not contain any element is called Empty set, or null set or void set.

Empty set is denoted by { } or ∅ (Greek letter phi).
which shows that there is no element in a set.

Example:

a. The set of natural numbers less than 0, 

we know that there is no natural number less than 0.
Therefore, it is an empty set. 

Cardinality of an empty set

The cardinality of an empty set is 0 (zero), i.e., the number of elements is zero.

A = {} or (phi) ∅

∴ n(A) = 0

The finite set is a set having countable number of elements and an empty set have zero element in it, and it is definite number of elements.

So, the empty set is a finite set with a cardinality of zero.

sometimes it may possible that the number of elements in a set is very big, but it is countable or it has starting and end point then is a non empty finite set. 

For example  A = {3, 4, 5, 6, 7………90}

Infinite Set 

If a set contains unlimited or (uncountable) number of elements is called an Infinite Set. Or if we can not count the number of elements of a set then it is called infinite set.

A set which is not a finite set is known as infinite set.

Example : (i) The set of natural numbers N is an Infinite Set.

                   N = {1, 2, 3, 4…} 

(ii) The set of whole numbers W is an Infinite Set.

                  W = {0, 1, 2, 3, 4…} 

(iii) The set of integers Z is an Infinite Set.

                  Z = {…-3 -2, -1, 0, 1, 2, 3, 4…}

(iv) Set of all points in a plane is an infinite set.

(v) Set of all points in a circle is an infinite set.

There is no end of counting numbers, set contains unlimited or uncountable number of elements. 

We can not represent an infinite set in roster form easily because its elements are not limited or countable, so, we use three dots (ellipses) to represent the infinity of a set.

N is a set of all natural numbers starting from one. 

The number of elements of this set is not countable, so we use three dots to represent its infinity.                              

Z is a set of all integers, its elements are also not countable, so we use three dots both sides for the infinity of negative and positive integers.  

                Cardinality of a infinite set

The cardinality of a set X is n(X) = a, where a represents the number of elements of set X.

We know that the number of elements in an infinite set is unlimited so the cardinality of an infinity set is n (A) = ∞, i.e., infinite.

           Properties of infinite sets

1.The union of two infinite sets is infinite.
2.The super set of an infinite set is also infinite.
3. The power set of an infinite set is infinite.

We know that the number of elements in an infinite set is unlimited so its power set and super sets also need to be infinite.

Presentation of sets in Venn diagram

1. Union of sets

If set A = {a, b, c, p} and Set B = {r, m, n, s}

∴  A∪B = {a, b, c, p, r, m, n, s}, so union of finite sets are also finite.

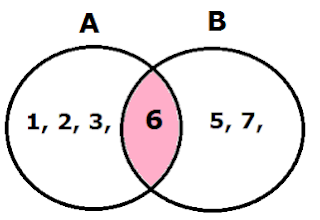
2. Intersection of sets

If set A = {1, 2, 3, 6} and Set B = {5, 7, 6,}

∴  A∩B = {6}, so intersection of finite sets are also finite.

If set A = {1, 2, 5, 7, 8} and Set B = {4, 7, 6, 8}

∴  A∩B = {7, 8}