Triangle – Word Problems – Sum of the Angles
Sum of the Angles of a Triangle Word problems
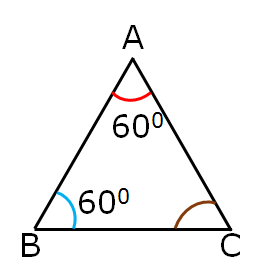
Problem (1) In the below figure find m∠C.
Solution: Sum of three angles in any triangle = 1800
∴ m∠A + m∠B + m∠C = 1800
600 + 600 + m∠C = 1800
1200 + m∠C = 1800
1800 – 1200 = m∠C
m∠C = 1800 – 1200
Therefore, m∠C = 600
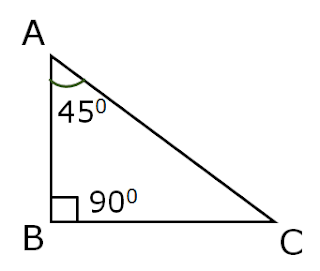
Problem (2) In the below figure find m∠C.
Solution: Sum of three angles in any triangle = 1800
∴ m∠B + m∠ + m∠C = 1800
900 + 450 + m∠C = 1800
1350 + m∠C = 1800
1800 – 1350 = m∠C
m∠C = 1800 – 1350
Therefore, m∠C = 450
Problem (3) Can 450 , 550 and 850 be the angles of a triangle.
Solution: Sum of three angles in any triangle = 1800
∴ m∠1 + m∠2 + m∠3 = 1800
∴ 450 + 550 + 850 ≠ 1800
Here sum of three angles of triangle is not equal to 1800
Therefore the given three angles can not be angles of a triangle.
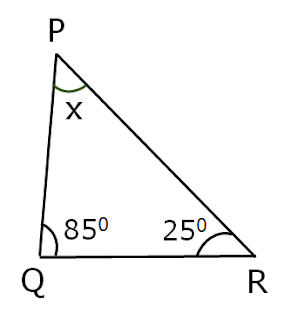
Problem (4) In the below figure find the value of x.
Solution: Sum of three angles in any triangle = 1800
∴ m∠P + m∠Q + m∠R = 1800
m∠x + 850 + 250 = 1800
1100 + m∠x = 1800
1800 – 1100 = m∠x
m∠x = 700
Therefore, m∠x = 700
Problem (5)Two angles of a triangle are 350 and 550 . find third angle.
Solution: Sum of three angles in any triangle = 1800
∴ m∠1 + m∠2 + m∠3 = 1800
350 + 550 + m∠3 = 1800
900 + m∠3 = 1800
1800 – 900 = m∠3
m∠3 = 900
Therefore, m∠3 = 900
Problem (6) One of the angles of a triangle is 1000
and the other two angles are equal. find the measure of each of the equal angles.
Solution: Sum of three angles in any triangle = 1800
∴ m∠1 + m∠2 + m∠3 = 1800
One angle is 1000 so sum of other two angles
are 800 . But, other two angle are equal.
Therefore each angle will be 80/2 = 400
∴ m∠1 + m∠2 + m∠3 = 1800
1000 + m∠2 + m∠2 = 1800
1000 + 2 m∠2 = 1800
1800 – 1000 = 2 m∠2
2 m∠2 = 800
2 m∠2 = 800 ÷ 2 m∠2 = 400
Therefore, m∠2 = 400
Problem (7) The three angles of a triangles in the ratio 1 : 2 : 3. Find all the angles of the triangle.
Solution: Form the ratio 1 : 2 : 3, the angles are x, 2x and 3x.
Sum of three angles in any triangle = 1800
∴ m∠x + m∠2x + m∠3x = 1800
m∠6x = 1800
m∠x = 1800 ÷ 6 m∠x = 300
Therefore, angles are m∠x = 300
m ∠2x = 2 x 300
m ∠2x = 600
m ∠3x = 3 x 300
m ∠3x = 900
Hence, angles are 300 , 600 and 900.