Subtraction of Like Fractions

Arithmetic operations addition, subtraction, multiplication and division can be preformed on fractions.

Fractions represents a part of a whole. The normal subtraction of numbers and the subtraction of fractions are different.

A fraction has a numerator and a denominator which is separated by a bar.

For example, 3/2, 4/7, 22/5, 26/7, 46/3.

There are two types of fractions. Like fractions and unlike fractions.

It is very easy to subtract the like terms.

Like fractions have a common denominators and unlike fractions have different denominators.

Example: 5/2 and 8/2 are like fractions.

In the given fractions denominator is same(2) these fractions are called like fractions.

Let us see more about subtraction of like fractions in this tutorial.

How to Subtract Like Fractions

We know that a fraction has two parts, the numerator and the denominator.

A general fraction is represented in the form of a/b, where a is the numerator and b is the denominator, and b cannot be zero.

The subtraction of like fractions is same as finding the subtraction of two or more fractions.

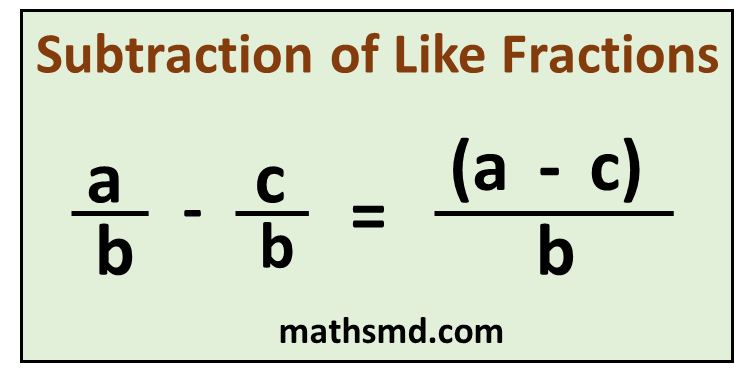
Subtraction of fractions with common denominators

There are 3 steps to subtract fractions

Step 1: Like fractions have common(Bottom numbers) denominators. First make sure that the denominators(bottom numbers) are same.

Step 2: Subtract the (numerators)top numbers of the fractions and put the answer over the same denominator.

Step 3: Simplify the fraction to its lowest form, if needed.

The subtraction of fractions is easy when they have a common denominator.

Let us learn the steps of subtraction of like fractions with the help of an example given below.

Example: Subtract 5/6 – 3/6

The above figure shows the subtraction of (5/6 – 3/6) fractions.

Here, 5/6 indicates that 5 out of 6 parts are shaded and 3/6 indicates that 3 out of 6 parts is shaded.

So, the subtraction of shaded parts is (5/6 – 3/6), is equal to 2/6.

In this example, we subtract only the numerators and keep the denominators as 6.

We write it as 5/6 – 3/6 = (5 – 3)/6 = 2/6.

So the answer of 5/6 minus 3/6 is 2/6.

We observe the figure, we can see that out of 6 parts, 2 parts are shaded. The fractional form of this can be represented as 2/6.

So, the subtraction of given fractions is 2/6.

Example: Solve 6/5 – 4/5

Here, denominators are same as 5, so we subtract numerators (6 -4)

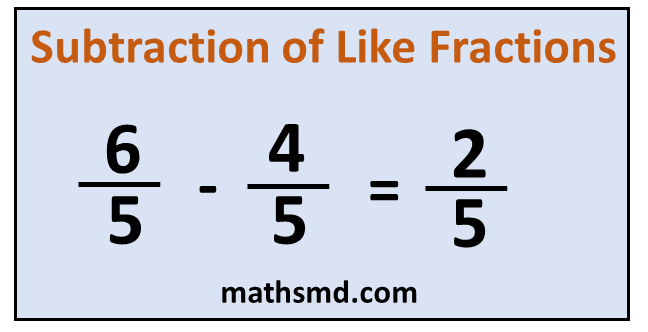
= (6 – 4)/5

= 2/5

Example: 8/3 – 7/3

= (8 – 7)/3

= 1/3.

Example: 9/5 – 6/5

= (9 – 6)/5

= 4/5

So the final answer is 4/5.

Example: 37/9 – 10/9

= (37 – 10)/9

= 27/9

Here, the numerator and denominator both are divisible by 3 and 9. However we always want to reduce the fraction by greatest common factor. Thus, greatest common factor is 9. Divide the numerator and denominator by 9 we get

= 27/9 = 3/1

So the final answer is 3/1