Concave Polygons: Definition – Examples & Properties  

All polygons is either convex or concave. A polygon will be convex or concave, it depends on the measure of their angles.

What is a Concave Polygon?

A concave polygon have at least four sides, and concave polygon is just opposite of a convex polygon.

If the measures of at least one angle of a polygon is more than 180⁰ than the polygon is concave, otherwise the polygon is convex.

                       Concave polygon

Definition: 

If a polygon has one are more interior angles, is greater than 180⁰ then it is called a concave polygon.

A concave polygon has one are more interior angles is greater than 180º, but a convex polygon has all the interior angles less than 180º.

Examples of concave polygons

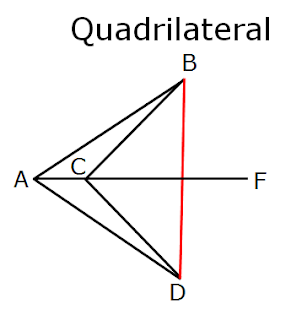
In above quadrilateral ABCD, diagonal BD is outside of the polygon, so it is a concave polygon.

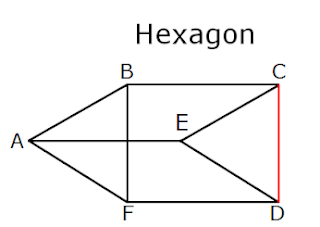
In above hexagon ABCDEF, diagonal CD is outside of the polygon, so it is a concave polygon.

Note- A triangle can never be a concave polygon, because it has only three sides and the total of it’s interior angles is 180^0, so none of any interior angle is greater than 180^0.

            Perimeter of a concave polygon

The perimeter of any polygon is defined by total length of it’s all sides covered around the boundary of the polygon.

Similarly, the perimeter of concave polygon is defined by total length of it’s all sides covered around the boundary of the concave polygon.

So, when we add length of all sides of a concave polygon, we get the perimeter of that concave polygon.

          Exterior angle of a concave polygon

Exterior angle of a concave polygon is always 360^0.

          Interior angle of a concave polygon

Sum of the measure of interior angles of a concave polygon is (n – 2)180^0.

Area of a concave polygon

^{There is no formula to find the area of a concave polygon. Each side of a concave polygon can be a different length and each interior angle can be different measure.} 

So, find the area of a concave polygon, we have to split the concave polygon as triangles, rectangles or parallelogram or any other shapes and we can easily find the area by using the formula of that shape.

In a concave polygon, certain diagonals will lie outside of the figure or on it’s exterior.