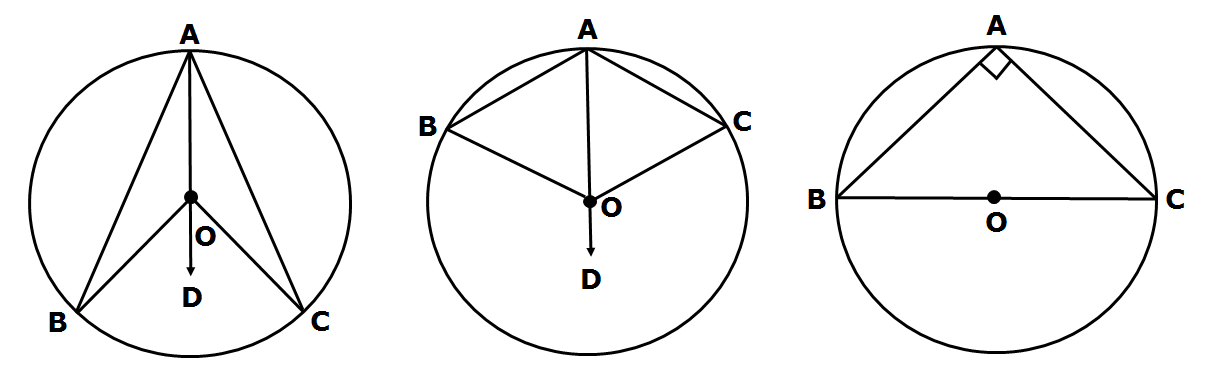
The angle at the centre of a circle is twice the angle at the circumference, when both are subtended by the same arc. 

Given: A circle with centre at O, arc BC of this circle subtends angles ∠BOC at centre O and ∠BAC at a point A remaining part of the circle.

 

To Proof: ∠BOC = 2 ∠BAC


Construction: Join AO and extend it to point B.


Proof: To prove this theorem we consider the arc BC in three difference situations.


1: Minor arc BC
2: Major arc BC  
3: Semi circle BC

Case 1: Minor arc BC

                       Adding 3 and 4


           ∠ DOB + ∠DOC = 2 (∠OAB + ∠OAC)


                        ∠BOC = 2 ∠BAC
            
                        or


In △ABO


OB = OA (radius of circle)

∴ ∠OBA = ∠OAB (angles opposite to equal sides are equal)…(1)


Also by exterior angle property exterior angle is sum of interior opposite angles.


∴ ∠DOB = ∠OBA + ∠OAB


∴ ∠DOB = ∠OAB + ∠OAB


∴ ∠DOB = 2 ∠OAB…(3)



In △ACO

OC= OA (radius of circle)

∴ ∠OCA = ∠OAC

(angles opposite to equal sides are equal)…(2)

Also by exterior angle property exterior angle is sum of interior opposite angles.

∴ ∠DOC = ∠OCA + ∠OAC

∴ ∠DOC = ∠OAC + ∠OAC

∴∠DOC = 2 ∠OAC…(4)  

                          Adding 3 and 4

∠ DOB + ∠DOC = 2 (∠OAB + ∠OAC)

                        ∠BOC = 2 ∠BAC

 

Case 2: Major arc BC 

In △ABO

OB = OA (radius of circle)

∴ ∠OBA = ∠OAB (angles opposite to equal sides are equal)…(1)

Also by exterior angle property exterior angle is sum of interior opposite angles.

∴ ∠DOB = ∠OBA + ∠OAB

∴ ∠DOB = ∠OAB + ∠OAB

∴ ∠DOB = 2 ∠OAB…(3)

In △ACO

OC= OA (radius of circle)

∴ ∠OCA = ∠OAC

(angles opposite to equal sides are equal)…(2)

Also by exterior angle property exterior angle is sum of interior opposite angles.

∴ ∠DOC = ∠OCA + ∠OAC

∴ ∠DOC = ∠OAC + ∠OAC

∴∠DOC = 2 ∠OAC…(4)  

                     Adding 3 and 4

∠ DOB + ∠DOC = 2(∠OAB + ∠OAC)

               ∠BOC = 2(∠OAB + ∠OAC)

      reflex ∠BOC = 2 ∠BAC

               ∴ reflex ∠BOC =  2 ∠BAC

Case 3: Semi circle BC 

 

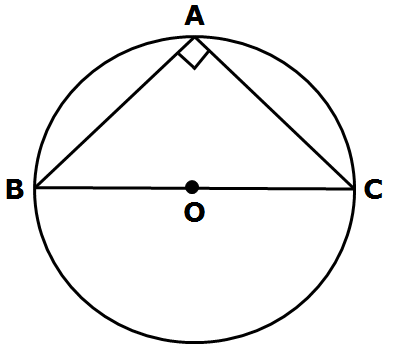
  BOC is a straight line passing through centre O.

 ∴ Angle subtended by arc BC at O is 180º

                ∴ ∠BOC = 180º …..(1)

The angle subtended by an arc at the centre is double of the angle subtended by it at any point on the remaining part of the circle.

                  Thus, ∠BOC = 2 ∠BAC

                      ∴ ∠BOC/2 = ∠BAC 

                       ∴ 180/2 = ∠BAC… from (1)

                      ∴ ∠BAC = 90º  
                                                   Hence Proved