Law of Exponents – Definition – Exponent Rules – Examples
Law of Exponents
In this chapter, we will study about law of exponents.
What is an Exponent?
When a number repeatedly multiplied by itself, multiple times is known as Exponent.
For example: p raised to q means that p is multiplied by itself q times.
= pq
= p x p x p x p x p…….q times.
Example: 5³ means multiply 5 by itself three times.
5³ = 5 x 5 x 5
Law of exponents or rule of exponents
Each rule of exponents shows how to add, subtract, multiply and divide exponents and how to solve different type of equations.
1. Multiplying Powers with Same Base
The general form of this rule is
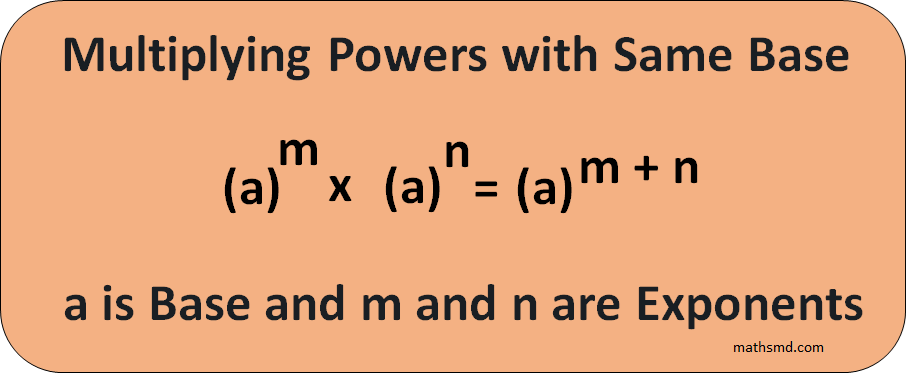
When multiplying two bases of the same values, then exponents are added together and keep bases remains same.Here, the base values are same as a, so keep them same and add the exponents (m+n) together.52 Power of two is called squared53 Power of three is called cubed.
Example: (i) 32 x 34
= (3 x 3) x (3 x 3 x 3 x 3)
Here, the base values are same as three, so keep them same and add the exponents (2 +4), so the addition of exponents are (2 + 4 = 6).
= 32 x 34
= 32 + 4
= 36
3 x 3 x 3 x 3 x 3 x 3 = 36
36 = 729
Then multiply 3 by itself 6 times to get the answer.
Example: 25 x 27
= (2 x 2 x 2 x 2 x 2) x (2 x 2 x 2 x 2 x 2 x 2 x 2)
= 25+7
= 212
Example: (-54) x (-57)
= [(-5) x (-5) x (-5) x (-5)] x [(-5) x (-5) x (-5) x (-5) x (-5) x (-5) x (-5)]
= (-5)4+7
= (-5)11
Example: (7/2)3 x (7/2)9
= [7/2 x (7/2) x (7/2)] x [(7/2) x (7/2) x (7/2) x (7/2) x (7/2) x (7/2) x (7/2) x (7/2) x (7/2)]
= (7/2)3 + 9
= (7/2)12
2. Division of powers with same Base
The general form of this rule is

When dividing two bases of the same value, keep the base same, and then subtract the exponents. In this equation the value of both bases are same as a, so subtract the exponents (m – n).
When dividing two bases of the same values, then subtracts the exponents and keep bases remains same. or
When exponents have same base, we subtract the exponents.
= 25 / 23
= 25 – 3
= 22
= 4
Example: (3 x 3 x 3 x 3 x 3)/(3 x 3 x 3)
= 35/33
= 35 – 3
= 32
= 9
In this equation the value of both bases same as three, and the exponents are 5 and 3. So subtract the exponents. Subtraction of (5- 3 =2). Then multiply 3 by itself 2 times (3 x 3 = 9 is the answer.
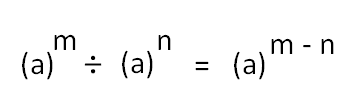
Example: (2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2)/(2 x 2 x 2 x 2 x 2 x 2 x 2)
= 29 – 7
= 22
Example: -58/-57
= [(-5) x (-5) x (-5) x (-5) x (-5) x (-5) x (-5) x (-5)] / [(-5) x (-5) x (-5) x (-5) x (-5) x (-5) x (-5)]
= – 58 – 7
= – 51
= – 5
Example: (7/3)9 / (7/3)4
= [7/3 x (7/3) x (7/3) x (7/3) x (7/3) x (7/3) x (7/3) x (7/3) x (7/3)] / (7/3)] x [(7/3) x (7/3) x (7/3)]
= (7/3)9-4
= (7/3)5
= (7/3)5
3. The law of multiplication of a powers with different bases but same exponents.

Example: (5 x 2)5
= (5 x 5 x 5 x 5 x 5)5 x (2 x 2 x 2 x 2 x 2)5
Here, exponents are same as 5 but bases are different that’s are 5 and 2.
= (5 x 2) x (5 x 2) x (5 x 2) x (5 x 2) x (5 x 2) [5 times]
= 10 x 10 x 10 x 10 x 10
= 100000
Example: (3 x p)4
= (3 x 3 x 3 x 3)4 x (p x p x p x p)4
Here, exponents are same as 4 but bases are different that’s are 3 and p.
= (3 x p) x (3 x p) x (3 x p) x (3 x p)
= 81p4
Example: = (7/2)3 x (7/5)3
= [(7/2) x (7/5)]3
When multiplying two exponents with same powers and different bases, the bases are multiplied. Mathematically it can be written as [an x bn = (a x b)n ]
4. The law of power of a power
This law implies that, when we raise a power to another power then keep the base same and multiply the exponents.
The general form of this rule is

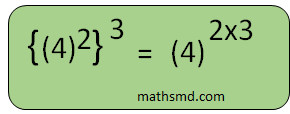
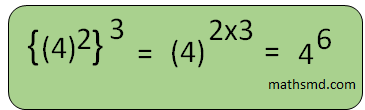
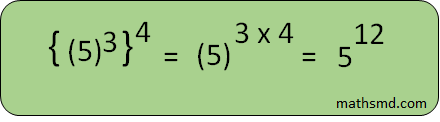
5. Law of Exponent Zero
The general form of this rule is

The exponent is zero with any base is equal to one.
Example: a0 = 1
Example: 20 = 1
Example: (3/2)0 = 1
Example: 3³/3³
= 33 ÷ 33
= (3 x 3 x 3)/(3 x 3 x 3) = 1
= 33-3
= 30
= 1
5³ ÷ 5³ = 5³/5³
= (5 x 5 x 5)/(5 x 5 x 5)
= 1
= 53-3
= 50
= 1
Example: 54 ÷ 54
= 54 – 4
= 50
= 1

6. The law of negative exponents
The general form of this rule is
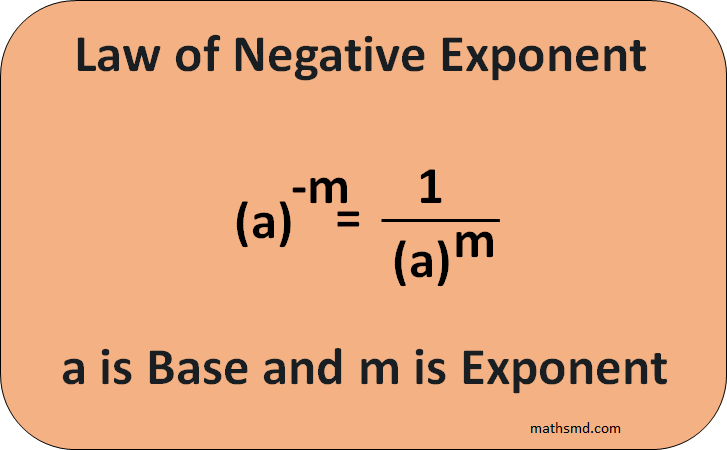
When an exponent is negative, we writing 1 in the numerator for change it into positive and get positive exponent in denominator.
a-n = 1/an
Example: 2-3 = 1/23
3-4 = 1/34
A number raised to a negative power is equal to the reciprocal of the power of exponent in the denominator.
When a base is raised to a negative power, find the reciprocal of the base keep the exponent with the original base and drop the negative.
7. The Law of Fractional exponents
In the fractional exponent, the general form is a¼= ∜a Where a is the base and 1/4 is the exponent.
The general form of this rule is

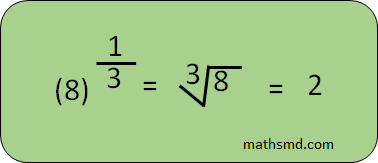
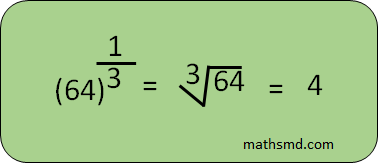
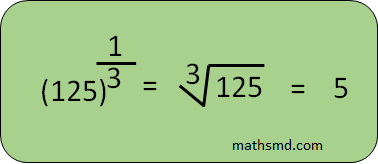
8. The law of Division of a powers with different bases but same exponents.
When dividing exponents with same powers and different bases, the bases are divided. Mathematically it can be written as
Here, we have two exponents with same power n and different bases a and b.
(a)m/(b)m = (a/b)m
The general form of this rule is
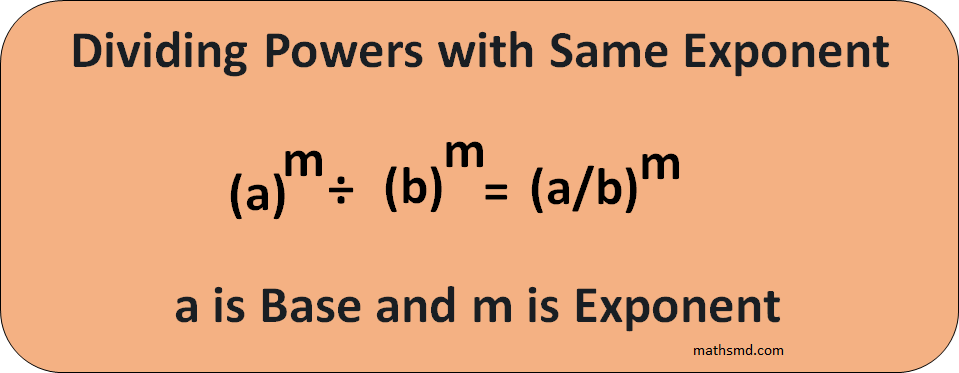
Example: [(2)5)/(3)5]
= (2/3)5
Example: [(7/3)6 ÷ (4/5)6]
= [(7/3)/(4/5)]6
Example: [(-5)4/24)
= (-5/2)4
=[(-5) x (-5) x (-5) x (-5)]/[(2) x (2) x (2) x (2)]

