Given: Two triangles △ ABC and △ ABD are on same base (or equal bases) AB, and area of △ ABC and △ ABD are equal.

Proof: CD ∥ AB

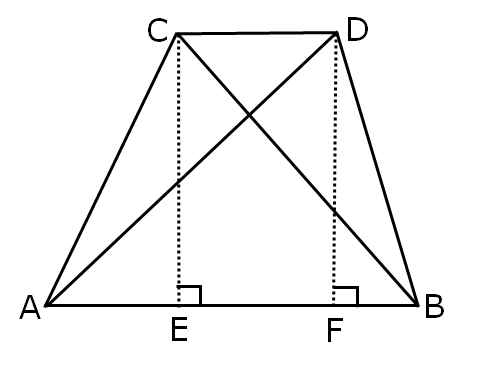
Construction: Draw CE and DF perpendicular to AB.
So DF is the height of △ ADB, and CE is the height of △ABC.

CE perpendicular to AB and DF perpendicular to AB.
Since, lines perpendicular to same line are parallel to each other

∴ CE ∥ DF….(1)

We know that Area of a triangle = 1/2 x Base x Height

In △ ABD, AB is base and DF is height.

∴ ar of △ ADB = 1/2 x base x height

= 1/2 x AB x DF…..(1) 

In △ ABC, AB is base and CE is height.

∴ ar of △ ABC = 1/2 x base x height

= 1/2 x AB x CE…..(2)

ar △ ADB = ar △ ABC 

From eq(1) and eq(2)

DF = CE…..(3)

Now DF and CE are perpendicular between the same parallel lines.

Now, in CDEF,

CE = DF and CE ∥ DF

Since one pair of opposite sides are equal and parallel.
Hence,

CDEF is a parallelogram.

So, CD ∥ EF

Since opposite sides of a parallelogram are parallel.

∴ CD ∥ AB

Hence Proved