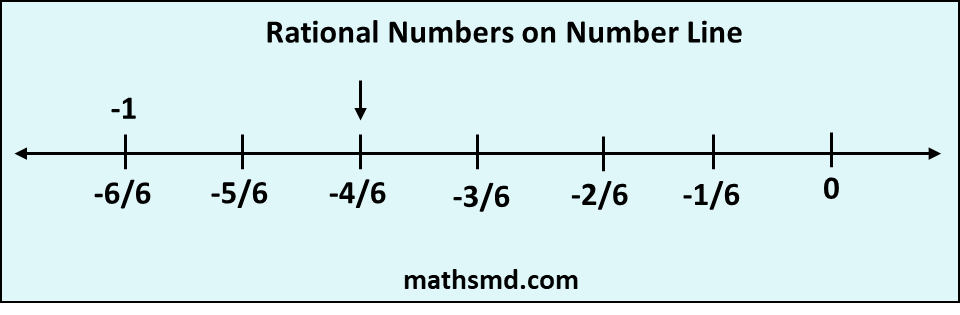Rational Numbers on Number Line

Rational Numbers

Rational numbers are numbers which can be represented in the form of p/q, where p and q are any two integers and q is not equal to zero(q ≠ 0).

Rational Numbers on Number Line

Rational numbers can easily represented on number line by following some simple steps.

Draw a line and locate the point 0. This point is center of the number line and is known as origin(0).

Representation of any rational number on number line is depend on the type of rational number.

Positive rational numbers are always represented on the right side of the origin(zero) on the number line.

Negative rational numbers are always represented on the left side of the (origin)zero on the number line.

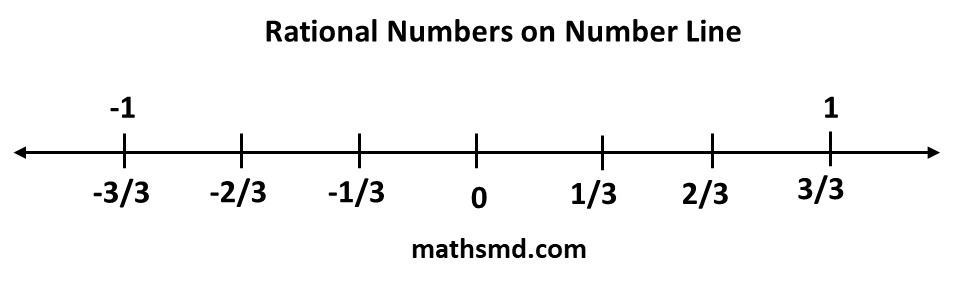
The representation of rational numbers can be classified into two different types.

(1) Proper fraction

(2) Improper Fraction

(1) Proper Fraction

A “Proper Fraction” is a fraction whose numerator is smaller than it’s denominator. Proper fractions are less than one and greater than zero.

Proper Fractions on Number Line

If it is a proper fraction, whose numerator is less than it’s denominator. So, proper fractions always exist between zero and one on number line.

Let us look some examples to understand the representation of positive rational numbers on number line.

First, we mark origin and integer value 1 on the number line. Now we divide this region into equal parts, such that these parts are equal to the denominator value. Then we mark the part with the value equal to the numerator.

For example we will draw 2/3 on number line. 2/3 is a proper fraction and 2/3 is greater than zero.

First we divide the number line between zero and one into 3 equal parts because denominator is 3, and the second part will be represented 2/3 on number line. It can be represented in below figure.

Representing negative rational numbers on the number line is similar to the representation of positive rational numbers, only the direction of movement is towards the left hand side of the origin. In below figure (-1/3) represents on number line.

(2) Improper Fraction

A “Improper Fraction” is a fraction whose numerator is greater than it’s denominator. Since, the numerator is greater than the denominator the number will be greater than one.

Improper Fractions on Number Line

For example we will draw 9/4 on number line. 9/4 is is an improper fraction and is positive.

When we represent such rational numbers on the number line first we convert the improper fraction into the mixed fraction. The conversion of mixed fraction(9/4) in the rational number will be 2 1/4, which means that the fraction would be between 2 and 3.

So first we will divide number line between 2 and 3 into 4 equal parts and then first part of 4 parts will be the required rational number on the number line.

Example: -9/4 is a given fraction is an improper fraction and is negative, so it will be lie on the left side of the number line.

When we represent such rational numbers on the number line first we convert the improper fraction into the mixed fraction. The mixed fraction of (-9/4) conversion of the rational number will be -2 1/4, which means that the fraction would be between -2 and -3.

So first we will divide number line between -2 and -3 into 4 equal parts and then first part of 4 parts will be the required rational number on the number line.

Example: We will draw -4/6 on number line. First we mark the origin and integer value -1 on the number line. rational numbers lie between 0 and -1.

Now we divide this region into 6 equal parts. To mark -4, move four parts on the left-side of zero.