Co-internal angles

Co-interior angles, also known as consecutive interior angles or same-side interior angles, are pairs of angles that lie on the same side of a transversal and inside the two lines it intersects. These angles have specific properties depending on whether the lines they intersect are parallel or not.

Definition and Identification

(1) Transversal Line:

A line that cuts across two or more (usually parallel) lines.

(2) Interior Angles: Angles that are on the inside of the two intersected lines.

When a transversal intersects two lines, it forms eight angles. The pairs of co-interior angles are the pairs of angles that are:

• On the same side of the transversal.
• Inside the two intersected line.

Properties of Co-Interior Angles

Non-Parallel Lines:

• When the two lines are not parallel, the co-interior angles do not have any specific relationship in terms of their measures.

Parallel Lines:

• When the two lines are parallel, the co-interior angles are supplementary. This means that the sum of the measures of the two co-interior angles is always 180º.
• If ∠A and ∠B are co-interior angles, then: ∠A+∠B=180

Example

Consider two parallel lines
l₁ and l₂ intersected by a transversal t:
Let’s label the angles formed at the intersections as follows:

In this diagram:

• ∠1 and ∠4 are co-interior angles.
• ∠2 and ∠3 are co-interior angles.

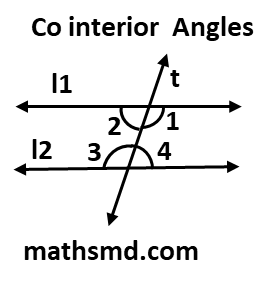
If l₁and l₂ are parallel, then:

∠1+∠4=180 and ∠2+∠3=180

Proof of Supplementary Property

When two parallel lines are cut by a transversal, corresponding angles are equal, and alternate interior angles are equal. This can be used to prove that co-interior angles are supplementary.

Let’s consider the same example:

• ∠1 and ∠2 are corresponding angles, so ∠1=∠2.
• ∠2 and ∠3 are alternate interior angles, so ∠2=∠3.
• Therefore, ∠1=∠3.

Since ∠3 and ∠4 form a straight line (linear pair), they are supplementary:

∠3+∠4=180

Substituting ∠1 for ∠3:

∠1+∠4=180

This proves that the co-interior angles
∠1 and ∠4 are supplementary.

Conclusion

Co-interior angles are a fundamental concept in geometry, especially when dealing with parallel lines and transversals. Understanding their properties helps in solving various geometric problems and proofs.