Alternate Exterior Angles – Definition – Examples and Properties

What are alternate exterior angles?

The term alternate exterior angles is often used when two lines are intersected by a third line(transversal).

Alternate exterior angles are formed when two lines are intersected by a third line. The third line is known as the transversal line.

Alternate exterior angles are the pair of angles that are formed on the outer side of the parallel lines but on the opposite side of the transversal.

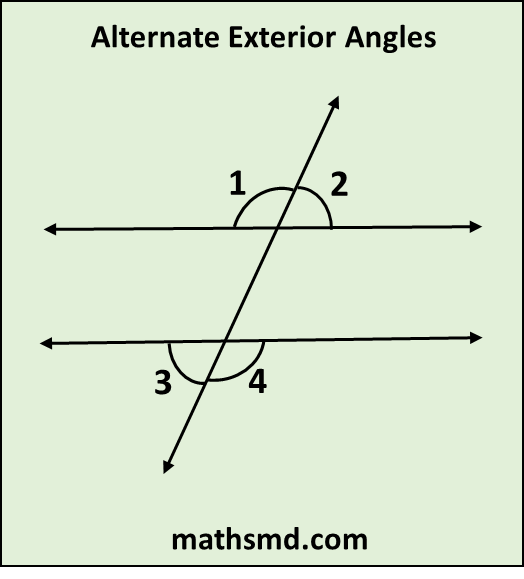
Definition:

The pair of non-adjacent angles with opposite side of the transversal line and on the outer or outside of the two parallel or non-parallel lines are known as alternate exterior angles.

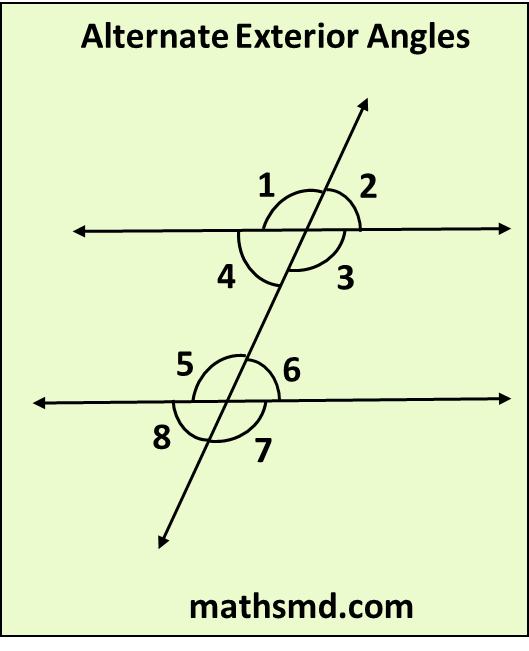
When two parallel or non-parallel lines are intersected by a transversal, they form eight (8) angles. Exterior angles are exist outside of the two lines.

In figure below, both ∠1 (angle 1) and ∠4 (angle 4) are a pair of alternate exterior angles because both angles are located on the outer side of the lines. They are also opposite side of the transversal and not adjacent to each other.

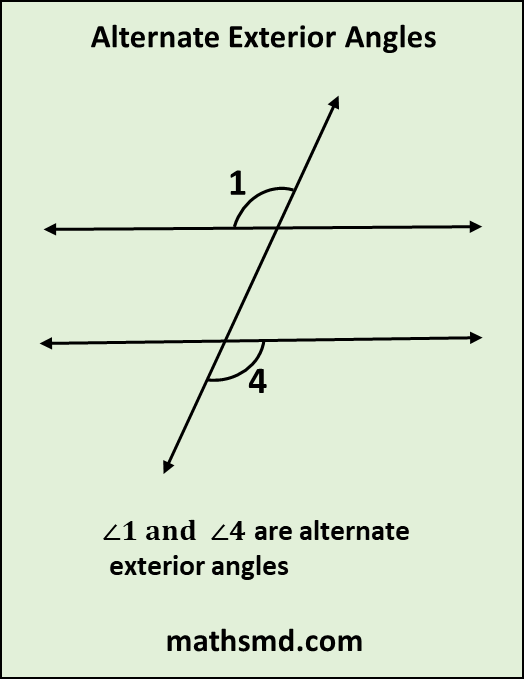
Hence ∠1 (angle 1) and ∠4 (angle 4) are a pair of alternate exterior angles.

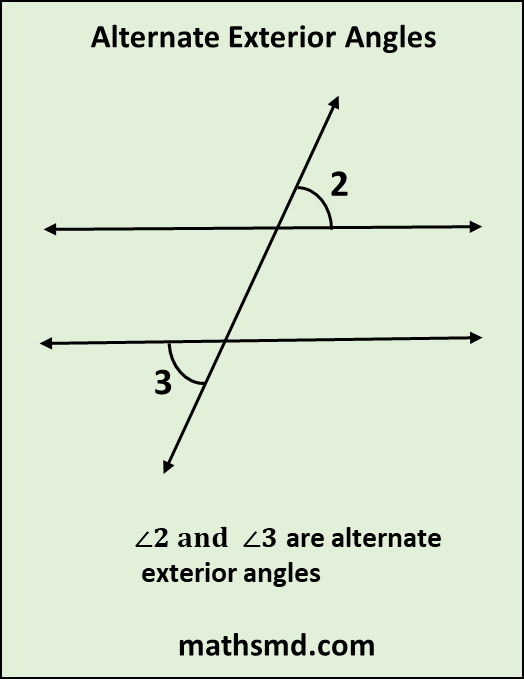
The other pair of alternate exterior angles is (angle 2) ∠2 and (angle 3) ∠3.

∠2 (angle 2) and ∠3 (angle3) are a pair of alternate exterior angles because both angles are located on the outside of the lines.

If two parallel lines are intersected by transversal line, then the pairs of alternate exterior angles are congruent.

If the alternate exterior angles are equal, then two lines are parallel.

Here transversal, intersecting two parallel lines. Since alternate exterior angles are congruent, both angles have same measure.

However, if a transversal intersects through two non-parallel lines, the pairs of alternate angles formed are not congruent and have no relationship in any way.

To understand more clearly what alternate exterior angles are, see the following properties.

Properties of Alternate Exterior Angles

• Alternate exterior angles are formed when a transversal intersect two parallel or non-parallel lines.

• When two line are parallel, the alternate exterior angles are same in measure(congruent).

• Consecutive exterior angles are supplementary (add up to 180)

• The sum of the angles formed on the same side of the transversal which are outside the two parallel lines is equal to 180.

• Alternate exterior angles are not congruent and have no any specific properties, when a transversal intersects two non-parallel lines.

Remember:

Pairs of alternate exterior angles are not only on opposite side of the transversal but also outside of the two lines.

Solved Examples

Question1: Is alternate exterior angles add up to 180º?

Answer: If the transversal intersects parallel lines then exterior angles are add to 180º (supplementary).

Question2: What does alternate exterior mean?

Answer: Alternate exterior angles are the pair of angles on the outer side of the two parallel lines but the opposite side of the transversal.