Power Set – Definition – Examples

Definition:            

 The Collection of all Subsets of a Given Set, is known as ‘Power Set’.

Power set of any set S is the set, of all subsets of S, including the empty set and set S itself.

Power set is denoted by P(S).

Example: For the set S = {1, 2, 3}

All the subsets of {1, 2, 3} are

1. The empty set {} or ∅ is a subset of {1, 2, 3}.

2. {1, 2, 3} itself is a is a subset of {1, 2, 3}.

3. {1,}, {2}, and {3} are subsets of {1, 2, 3}.

4. {1, 2}, {2, 3} and {1, 3} are subsets of {1, 2, 3}.

When we, list all the subsets of S = {1, 2, 3},
we get the Power Set of {1, 2, 3} so, 

P(S)= [{}, {1,2,3}, {1}, {2}, {3}, {1,2}, {1,3}, {2,3},].

                     Number of subsets in a set

If the original set has n elements, then the power set will have 2ⁿ  elements.

Example: In the above example there are three elements {1,2, and 3} so, the power set should be 

                               2³  = 8

The number of elements of a set is often written as 

   so, when S has n elements, we can write                           

Example: For the set S = {2,3,4,5,6} 

how many elements will the power set have?

S have 5 elements so, 

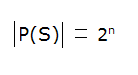
      = 2⁵

= 32