Sets and Venn Diagrams

The relationship between sets can be represented by diagrams is known as Venn Diagrams.

In venn diagrams, 

1. A rectangle is represent a universal set.

2. Circles or ovals are represent other subsets of the universal set.

Example: The set of Natural numbers is a subset of set of Whole numbers, which is a subset of Integers.

The set of Natural numbers is N, set of Whole numbers is W and set of Integers is Z

           let’s see above example in venn diagram,

Example: Let U = {a, b c, d, e, f, g, h} and  A =  {e, f, g, h}, in this example set U is the universal set, and set A is a subset. 

             we see these sets in venn diagram

Example: Let U = {a,b,c,d,e,f,g,} and  A =  {e,f,g,}, in this example set U is the universal set, and set A is a subset. 

             we see these sets in venn diagram

Example: Let U = {a, b, c, d, e, f, g, h, i, j} and  A =  {e, f, g, h}, in this example set U is the universal set, and set A is a subset. 

             we see these sets in venn diagram

A∪B

A∩B

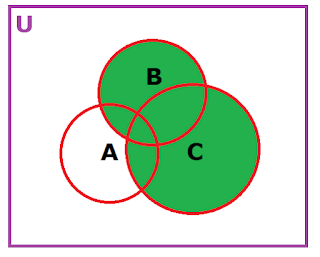
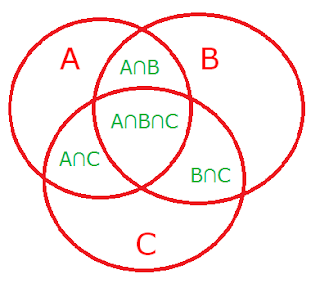
Venn diagram in three sets, A, B and C.

Venn diagram in two sets, A and B.

In above figure, Set A belongs element a, Set B belongs element c, Set A and set B both belongs element b,

(A∩B), m is the element belong None of sets A and B both.

∴ n(A) = a + b,

n(B) = b + c

n(A∩B) = b

n(A∪B) = a + b + c

Total number of elements = a + b + c + m

(B∪C)

A∩C

B∩C

A∪B

A∩B

Here are some basic formulas for venn diagram of two and three elements.

1.      n(A∪B) = n(A) + n(B) – n(A∩B)

2.      n(A∪B∪C) = n(A) + n(B) + n(C) – n(A∩B) – n(B∩C) – n(C∩A) + n(A∩B∩C)