Real Numbers – Definition and Examples

In this tutorial, we will learn all about real numbers.

What are Real Numbers?

Real numbers are the set of rational and irrational numbers in number system.

Real Number Definition

Real numbers are union of rational and irrational numbers. Real numbers can be represented on number line and all arithmetic operations can be performed on them.

Real numbers are denoted by symbol “R”.

Examples of real numbers are 12, 0, 6.15, 7/2 √3, √5, 𝜋 and so on.

The imaginary numbers are unreal numbers that cannot be expressed on the number line and is usually used to represent a complex number.

Subsets of Real Numbers

The following figure shows the relationship between all the numbers.

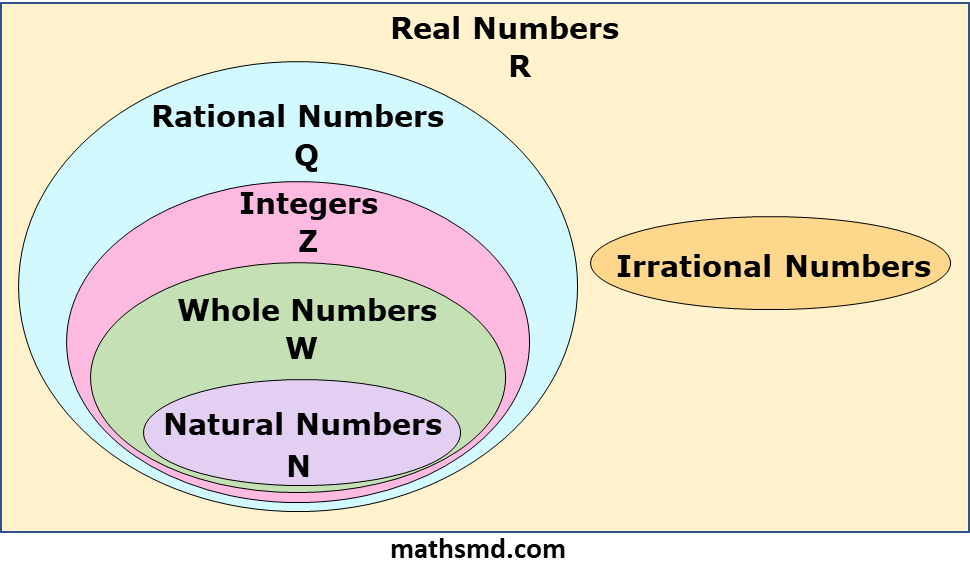
Real numbers have following subsets.

These sets N, W, Z and Q are subsets of R.

This shows that real numbers include natural numbers, whole numbers, integers, rational numbers, irrational numbers.

Real numbers are the combination of rational and irrational numbers.

Rational Numbers are divided into two categories.

Rational numbers and Irrational numbers.

Rational Numbers: Any number that can be written in the form of a fraction a/b, where ‘a’ and ‘b’ are both integers and b ≠ 0.

A rational number can be a nature number, a whole number, a decimal, a fraction.

Example: 1/2, o.5, 8/5, 14/7.

Rational numbers can be divided into

Natural Numbers: Natural numbers are counting numbers. Natural Numbers including all positive integers from 1 to infinity.

Set of Natural Numbers, N = {1, 2, 3, 4, 5….}

Whole Numbers: A set of numbers including natural numbers, and 0 is called whole numbers.

Set of whole numbers, W = {0, 1, 2, 3, 4, 5….}

Integers: All positive and negative numbers including zero (not fractions) are called Integers.

Z = {….., -3, -2, -1, 0, 1, 2, 3, 4, 5…..} (-∞ to +∞ )

Irrational Numbers: Irrational numbers are the set of real numbers that can not be expressed in the form of a fraction or ratio of two integers. a/b where ‘a’ and ‘b’ integers and the denominator ‘b’ is not equal to zero(b ≠ 0).

For example pi is an irrational number. The value of 𝜋 (pi) in decimal is 3.14159265… but in this case no finite number of digits can represent the value of 𝜋 exactly and not does it repeat.

Therefore, the numbers like (√2, 𝜋 , √3, 5 etc.) are irrational numbers.

Which are not real numbers?

The numbers that are neither rational nor irrational are non-real numbers. Example: i, √-3, 3 + 2i,.

These numbers are not real numbers. These numbers are called complex numbers.