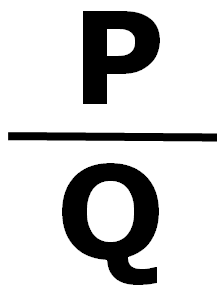What are Rational Numbers ?

Rational numbers are a fundamental concept in mathematics. Here is a detailed explanation of rational numbers:

The word comes from “Ratio”, means comparison of two or more numbers.

The natural numbers, whole numbers and integers all are the set of a rational number means any number that can be rewritten in the form of a simple fraction is a rational number.

Natural numbers

All positive integers like 1, 2, 3, 4… are natural numbers.

Whole numbers

All natural numbers including 0 are whole numbers.

Integers

All negative and positive numbers including 0 are known as integers.

Rational numbers

Rational numbers include all natural numbers, whole numbers, integers and fractions.

Definition:

In mathematics a rational number is a number which can be written in the form p/q, where p is and q are integers and q ≠ 0, p is numerator and q is non zero denominator. The denominator in a rational number cannot be zero.

Example:  2/3, -5/4, 6/1, all are Rational Numbers.

• 3 is a rational number because it can be written as 3/1.
• The number 2/3 is a rational number because in this number integer 2 is divide by integer 3. 
• 7/5 is a rational number because in this number integer 7 is divide by integer 5.
• 0/0 is not a rational number because there is zero in the denominator.
• The number 7 is a rational number because in this number integer 7 is divide by integer 1.
• 0.2 is a rational number because it can be rewritten as 1/5.
• 0.25 is a rational number because it can be rewritten as 1/4.
• 0.75 is a rational number because it can be rewritten as 3/4.
• 0.33333… is a rational number because it can be rewritten as 1/3.
• 1/2 (one-half) is a rational number because it can be expressed as a fraction of two integers.
• −3/4 (negative three-fourths) is also a rational number.
• 5 is a rational number because it can be written as 5/1.
• 0 is a rational number because it can be written as 0/1.

Note:

• All integers are rational numbers.
• Zero is a rational number because it can be rewritten as 0/1.

Properties of Rational Numbers

Closed under Addition, Subtraction, Multiplication, and Division (excluding division by zero):

If, a, b, c, and d are integers with b≠0 and d≠0 then:

Addition: a/b + c/d is a rational number.

Subtraction: a/b − c/d is a rational number.

Multiplication: a/b × c/d is a rational number.

Division: a/b ÷ c/d (where, b≠0 and d≠0) is a rational number.

Density:

Rational numbers are dense in the real numbers. This means that between any two rational numbers, there is another rational number.

For example, between 1/2 and 2/3, there is 5/9, and between any two rational numbers, we can always find more.

Decimal Representation:

Rational numbers can be represented as either terminating decimals (e.g.,1/4=0.25) or repeating decimals (e.g.,1/3=0.333…).

Comparison with Other Number Sets

Integers: All integers are rational numbers because any integer n can be written as n/1.

Real Numbers: Rational numbers are a subset of real numbers. Real numbers include both rational numbers and irrational numbers (numbers that cannot be expressed as a fraction of two integers, like ✓2 or π).

Irrational Numbers: These are numbers that cannot be expressed as a ratio of two integers. Their decimal expansions are non-terminating and non-repeating.

Examples include π, ✓2, and e. Visualization.

On a number line, rational numbers include all the points that can be expressed as fractions or integers. They form a dense set, meaning that there is no gap between them when considering the infinite number of rational numbers between any two given points.

In short A rational number is any number that can be expressed as the quotient or fraction a/b of two integers.

Where a (the numerator) and b (the denominator) are integers, and b≠0.

In other words, a rational number can be written as:
a/b where, a and b are integers, and b≠0.

Summary

Rational numbers are numbers that can be expressed as the fraction of two integers with a non-zero denominator. They have properties that make them closed under the basic arithmetic operations and are densely packed on the number line, meaning there are infinitely many rational numbers between any two given rational numbers. Their decimal representations are either terminating or repeating.