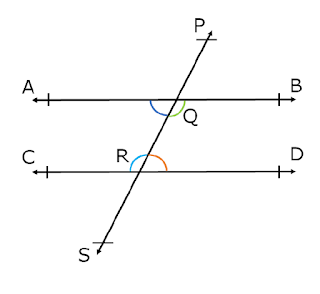
Theorem – Alternate Interior Angles are Equal 

If a transversal intersects two parallel lines, then each pair of alternate interior angles are equal.

Given: Two parallel Lines AB and CD, and PS be transversal intersecting AB at Q and CD at R.

To Prove: Each pair of alternate interior angles are equal.

i.e. ∠BQR = ∠CRQ and ∠AQR = ∠QRD

Proof: Parallel lines AB and CD, and PS be transversal
intersecting AB at Q and CD at R.

So that, ∠AQP = ∠CRQ (Corresponding angles)….1

For lines AB and PS 

∠AQP = ∠BQR  (Vertically opposite angles)….2

From (1) and (2)

∠BQR = ∠CRQ

Hence pair of alternate interior angles are equal.

Similarly we can prove that

∠AQR = ∠QRD

                                           Hence proved.