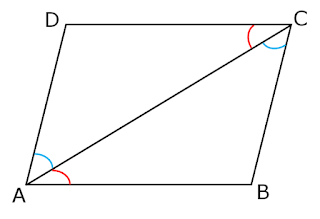
In a parallelogram opposite sides are equal. 

Given: A parallelogram ABCD, each pair of Opposite sides of parallelogram are side AB and side DC and side AD and side BC.

To prove: Opposite sides of parallelogram are equal that is

AB = DC    and    AD = BC 

Construction: Join A to C that is AC, is a diagonal, the diagonal AC divides parallelogram ABCD into two triangles △ ABC and △ CDA.

Proof: In △ ABC and △ CDA

BC ∥ AD and AC is a transversal.

So, ∠BCA = ∠DAC (Alternate angles of parallel sides)

Similarly, AB ∥ DC and AC is a transversal.

So, ∠BAC = ∠DCA (Alternate angles of parallel sides)

and AC = CA (Common)

These triangles △ ABD and △CDA are congruent,

                      △ ABC ≅ △CDA 

So, △ ABC ≅ △CDA (By ASA rule)

or diagonal AC divides parallelogram ABCD into two congruent triangles △ ABC and △ CDA.

So, the corresponding sides of triangles △ ABC and △ CDA are equal.          

 So,        AB = DC    and    AD = BC

   Hence proved.