Definition, Properties, Examples – Cyclic Quadrilaterals

What is a Cyclic Quadrilateral

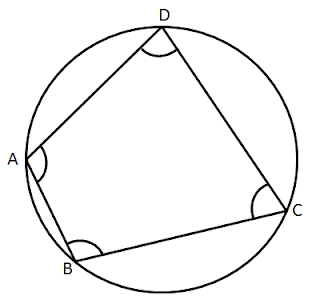
A cyclic quadrilateral is a four sided polygon that is inscribed in a circle. The vertices are said concyclic. The center of the circle is called circumcenter and radius of the circle is called circumradius.

Definition: A Cyclic Quadrilateral is a quadrilateral, whose all four vertices pass through the circle or touch the circumference of circle.

In above figure the circle drawn passing through all four vertices of quadrilateral A, B, C and D, so the quadrilateral is called as Cyclic Quadrilateral.

Properties of Cyclic Quadrilateral

The properties of a Cyclic Quadrilateral are as follows.

(1) The sum of a pair of opposite angles of a cyclic
quadrilateral is 180º (supplementary). or

Opposite angles of a Cyclic Quadrilateral are supplementary.

i.e.          ∠A + ∠C = 180⁰
and      ∠B + ∠D = 180⁰

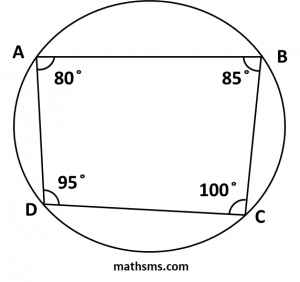
(2) If two opposite angles of a quadrilateral are supplementary, then it is a cyclic quadrilateral.

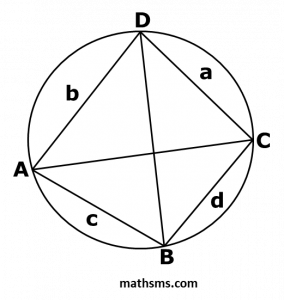
(3) When ratio of the diagonals and the ratio of the sum of products of the sides that share the diagonal’s end points are equal, then it is cyclic quadrilateral.  

(4) In a cyclic quadrilateral Perpendicular Bisectors are concurrent.

(5) In a cyclic quadrilateral, four equal Bisectors of four sides meet at the center of the circle.

(6) In a cyclic quadrilateral if one side of the cyclic quadrilateral is produced, then the measure of exterior angle is equal to the opposite interior angle.

(7) The four sides of the inscribed quadrilateral are four chords of the circle.

The area of a cyclic quadrilateral = √(s – a)(s – b)(s – c)(s – d)

Where a, b, c and d are the four sides of the quadrilateral and s is the semi perimeter.

Where s = 1/2 x (a + b + c + d)