Prove that the angle in a semicircle is a right angle – Theorem – Geometry

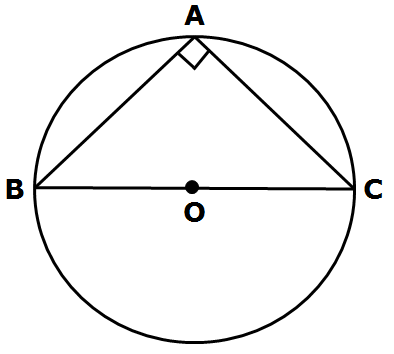
Prove that the angle in a semicircle is a right angle 

                         or

Angle subtended by a diameter/Semicircle on any circle on any point of circle is 90º.

Given: A circle O with centre O. BC is the diameter of circle subtending ∠BAC at point A on circle.

To Prove: ∠BAC = 90º 

 

Proof: 

  BOC is a straight line passing through centre O.

 ∴ Angle subtended by arc BC at O is 1800

∴ ∠BOC = 180º      ….(1)

The angle subtended by an arc at the centre is double of the angle subtended by it at any point on the remaining part of the circle.

                  Thus, ∠BOC = 2 ∠BAC

                      ∴ ∠BOC/2 = ∠BAC 

                       ∴ 180/2 = ∠BAC… from (1)

                      ∴ ∠BAC = 90º
  
                                                   Hence Proved

Related posts:

  1. The angle subtended by an arc at the centre is double of the angle subtended by it at any point on the remaining part of the circle – Theorem – geometry
  2. Theorem – The perpendicular from the center of a circle to a chord bisects the chord
  3. Theorem – The perpendicular from the center of a circle to a chord bisects the chord
  4. Square – Properties – Formula – Geometry
  5. Parts of a Circle – Definition, Examples and Formula – Radius – Diameter – Chord – Circumference – Arc – Area – Sector –
  6. Circle Worksheet
  7. Arc – Definition & Example – Arc length Formula – Geometry
  8. Protractor – How to measure angle with Protractor – Geometry
  9. Types of quadrilaterals – Definition – Properties
  10. Types Of Angles – (Acute, Right, Obtuse, Straight, Reflex, Complete Angles)

Leave a Reply

Your email address will not be published. Required fields are marked *