Parallelograms on the same base and between the same parallels are equal in area.

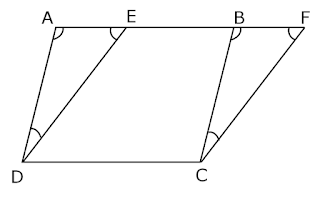
Given: Two parallelograms ABCD and EFCD, are on the same base DC and between the same parallel lines AF and DC.

To prove: area (∥gm ABCD) = area (∥gm EFCD)

Proof: In △ AED and △ BFC

BC ∥ AD and AF is a transversal.
So, ∠DAE = ∠CBF …..(1) (Corresponding angles of parallel sides)

Similarly, ED ∥ FC and AF is a transversal.
So, ∠AED = ∠BFC …(2) (Corresponding angles of parallel sides)

Therefore,  ∠ADE = ∠BCF …(angle sum property of a triangle)….(3) and

AD = BC (opposite sides of parallelogram ABCD)….(4)

So triangles △ ADE and △BCF are congruent,

△ ADE ≅ △BCF (using (1), (3) and (4) So, 

△ ADE ≅ △BCF (By ASA rule)

Therefore,   ar △ADE = ar △BCF (congruent figures have equal areas)…(5)

Now, ar (∥gm ABCD) = ar (△ ADE) + ar (quadrilateral EDCB)

                               = ar (△ BCF) + ar (quadrilateral EDCB)…from (5)

                              = ar (∥gm EFCD)

So, parallelogram ABCD and EFCD are equal in area.

             ar (∥gm ABCD) = ar (∥gm EFCD)

                    Hence proved.