SSS, SAS, ASA, AAS and RHS – Congruence of Triangles 

In geometry we see that, if two line segments are are same in length, they are congruent, and if two angles are same in measure they are also congruent,.
Simply,

we can say congruent means an object and its mirror image.

Congruence Triangles

A triangle is a polygon with three line segments and three vertices.

Two triangles are congruent, if they have same size and same shape, means their sides have same length and their interior angles have same measure.

Thus, two triangles are congruent if they are copies of each other and when superposed, they cover exactly each other.

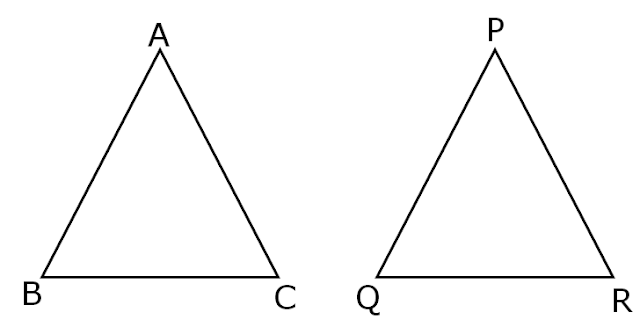
Two  triangles △ ABC and △ PQR have same shape and same size.

           △ ABC and △ PQR are congruent.

Congruent is denoted by symbol  ≅  we can say,

                      △ ABC ≅  △ PQR

So, when we place △ PQR on △ ABC, vertex P falls on   vertex A, vertex Q falls on vertex B and vertex R falls on vertex C.

Corresponding Vertices :   A and P,   

B and Q  and   

C and R.

Side PQ on Side AB, 

QR on side BC and

side PR on side AC.

If two line segments have same or equal length, they are congruent, and its opposite,
if  two line segments are congruent, they have same or equal in length.
When two line segments AB and CD are congruent we write,

                                 AB = CD

                            or  AB ≅ CD

Corresponding Sides :      AB and PQ

                                   BC and QR                             

and   AC and PR. 

                               
Corresponding Angles :  

∠A and ∠P 

                                ∠B and ∠Q                         

and  ∠C and ∠R.

If two angle have same or equal measure, they are congruent, and its opposite, if two angles are congruent, they have same or equal in measure.

When two angles ∠A and ∠B are congruent we write, 

                            ∠ABC = ∠PQR
                       or  ∠ABC ≅ ∠PQR

Note : The order of the letters in the names of congruent triangles shows the corresponding relationship.

When we write        △ ABC ≅  △ PQR

it means that A lies on P, B on Q and C on R.
Side AB side PQ, side BC on side QR, and side AC on side PR. 

                      Congruence of Triangles 

(i)  SSS Congruence 

If three sides of a triangle are equal to the three correspondence sides of another triangle, then the triangles are congruent.

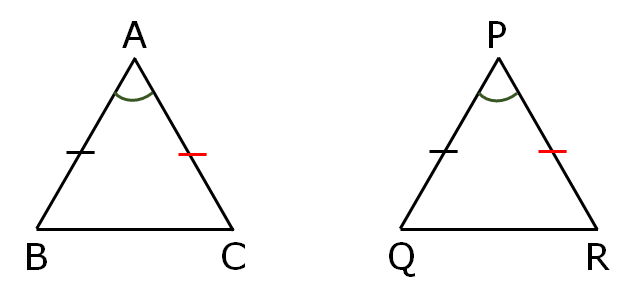
(ii)  SAS Congruence

If two sides and the angle included between them of a triangle are equal to two correspondence sides and the angle included between them of another triangle, then the triangles are congruent.

(iii)  ASA Congruence 

If two angles and the included side of a triangle are equal to two correspondence angles and the included side of another triangle, then the triangles are congruent.

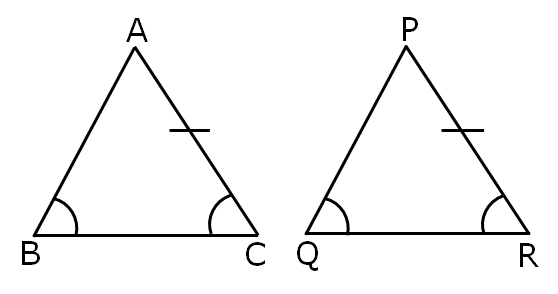
(iv)  AAS Congruence 

If two angles and a opposite side of a triangle, are equal to two correspondence angles and the correspondence side of another triangle, then the triangles are congruent.

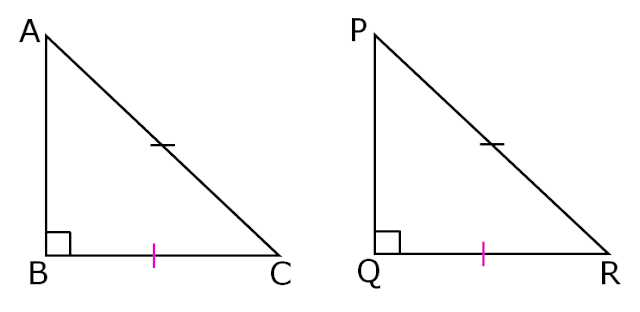
(v)  RHS Congruence 

If the hypotenuse and one side of a right angled triangle are respectively equal to the hypotenuse and one side of another right angled triangle, then the triangles are congruent.