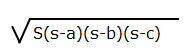Area of a Triangle – Geometry – Problems with Solutions
Area of a Triangle
In this lesson we will learn, how to calculate the area of a triangles with different formula’s. When given
1. The base and height of a triangle.
2. Two sides and one angle.
3. The length of three sides.
4. An equilateral triangle.
First we see about a triangle.
A triangle is a simple closed curve, with three line segments. It has three sides three vertices and three angles.
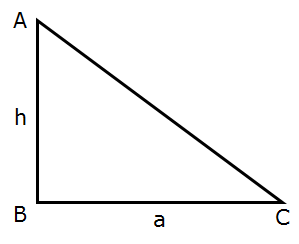
If we know the base, and perpendicular height of the given triangle then we can find the area of the triangle use the formula,
If we are given the base of the triangle and the perpendicular height then we can use the formula.
Area of a triangle = 1/2 x base x height
Area of triangle is equal to half of the product of its base and height.
The height of the triangle is the perpendicular distance from vertex to the base of triangle.
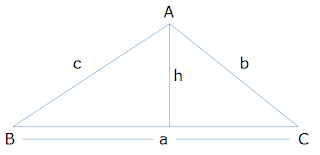
Formula for area of a triangle
Area of a triangle = 1/2 x base x height
Area of a triangle = 1/2 x ah
Where, a is the base of the triangle and h is the height of the triangle.
We can use any three sides as a base, it depends where height is drawn.
Example 1- Find the area of a triangle with a base 4 cm and height is 3 cm.
Solution: Given that base of triangle a = 4 cm
and height h = 3 cm
Area of a triangle = 1/2 x base x height
Area of a triangle = 1/2 ah
= 1/2 x 4 x 3
= 12/2
= 6 cm2
Solution: area of triangle = 6 cm2
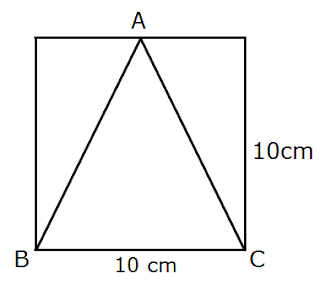
Example 2- In below figure △ ABC is inscribed inside a square of side 10 cm. Find the area of a triangle.
Solution: Given that ABC is inscribed inside a square of side 10 cm.
Therefore, the height of the triangle is 10 cm and also base of the triangle is 10 cm, because △ ABC is inscribed inside a square and a square has all sides of are equal.
base of triangle a = 10 cm
and height h = 10 cm
Area of a triangle = 1/2 x base x height
Area of a triangle = 1/2 ah
= (1/2) x 10 x 10
= 100/2
= 50 cm2
area of triangle = 50 cm2
Solution: area of triangle = 50 cm2
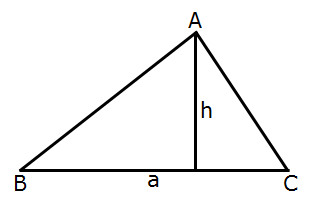
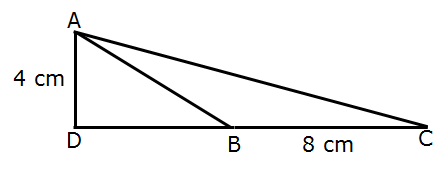
Example 3- In below figure given △ABC. Find the area of a triangle.
Solution: Given that base of triangle a = 8 cm
and height h = 4 cm
Area of a triangle = 1/2 x base x height
Area of a triangle = 1/2 ah
= 1/2 x 8 x 4
= 32/2
= 16 cm2
Solution: area of triangle = 16 cm2
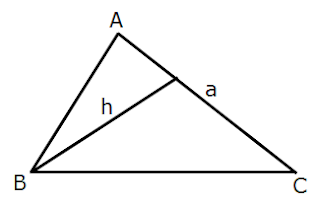
Example 4: In below figure given △ABC. Find the area of a triangle.
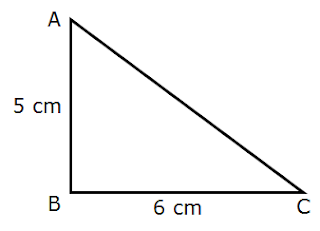
Solution: Given that base of triangle a = 6 cm
and height h = 5 cm
Area of a triangle = 1/2 x base x height
Area of a triangle = 1/2 ah
= 1/2 x 6 x 5
= 30/2
= 15 cm2
Solution: area of triangle = 15 cm2
The length of three sides
If given the length of three sides of a triangle, then we can use the formula to find the area of triangle.
Where a, b and c are length of three sides of triangle, and S is the half of total of a, b and c.
S = (a + b + c)/2
S is the half of the perimeter.
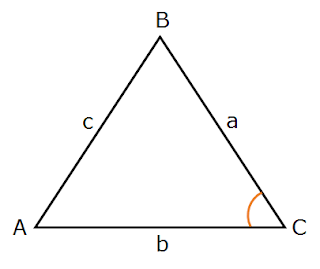
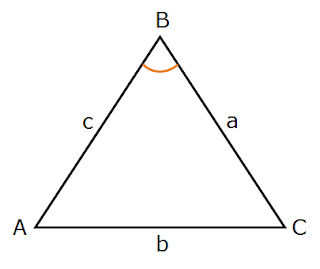
Two sides and one angle
If given the length of two sides of a triangle and measure of a angle between them then we can use the formula to find the area of triangle.
Area = 1/2 ab sin C
The area of triangle is equal to half of the product of two sides times the sine of the included angle.
Area = 1/2 ab sin C
Area = 1/2 ac sin B
Area = 1/2 bc sin A