Area – Definition – Formula – Example

let’s dive into the concept of area in math with a comprehensive explanation, formula, examples, and units.

Definition

Area is the amount of space inside the boundary of a two-dimensional shape. It is measured in square units, which represent the number of squares of a given size that can fit inside the shape.

Formula

The formula for calculating the area depends on the shape. Here are some common shapes and their area formulas:

1. Square: Area = side × side

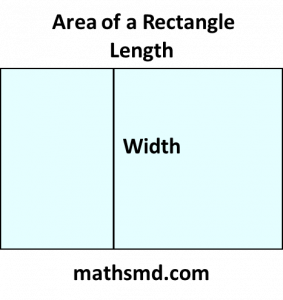
1. Rectangle: Area = length × width

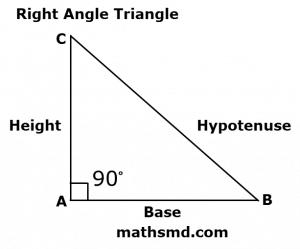
1. Triangle: Area = 1/2 × (base × height)

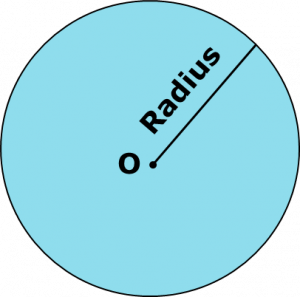
1. Circle: Area = π × radius²

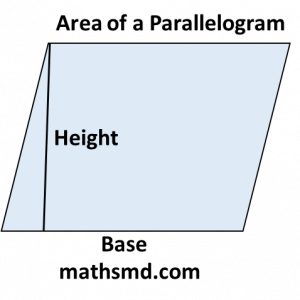
1. Parallelogram: Area = base × height

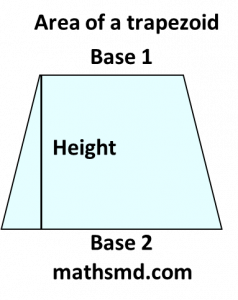
1. Trapezoid: Area=1/2 x (base1​ + base2​)×height

Examples

1. Square:
   • If the side of a square is 4 meters, the area is calculated as: Area = 4 m × 4 m = 16 m²
2. Rectangle:
   • If the length is 5 meters and the width is 3 meters, the area is: Area = 5 m × 3 m = 15 m²
3. Triangle:
   • If the base is 6 meters and the height is 4 meters, the area is: Area = 1/2 × (6 m×4 m ) = 12 m²
4. Circle:
   • If the radius is 3 meters, the area is: Area = π × 3 m × 3 m ≈ 28.27 m² (usingπ≈3.14)

Units

The units for area are always in square units. Here are some examples:

1. Square meters (m²)
2. Square centimeters (cm²)
3. Square kilometers (km²)
4. Square inches (in²)
5. Square feet (ft²)
6. Square yards (yd²)

Detailed Example

Let’s work through a detailed example for a rectangle.

Example: Find the area of a rectangle with a length of 8 meters and a width of 5 meters.

Solution:

1. Identify the length and width.
   • Length (l) = 8 meters
   • Width (w) = 5 meters
2. Use the formula for the area of a rectangle: Area = l × w
3. Plug in the values: Area = 8 m × 5 m = 40 m²

So, the area of the rectangle is 40 square meters.

Visual Representation

Imagine you have a rectangle drawn on graph paper, and each small square on the graph paper represents 1 square meter. You would count 40 of these small squares inside the rectangle, confirming that the area is 40 square meters.

Example: The rectangle have the sides are 5cm and 4cm so the area is

Area of rectangle = w x h

We find the area of a rectangle by multiplying widths times with height.

Area of rectangle = width x height

5 cm x 4 cm = 20 square centimeter.

                         = 20 cm²

In above rectangle, the area of the rectangle = 20 cm²

If any shape have different units, first convert them in same units.

Note: Area is measured in square units. If the sides in meter or feet the area would be square meter or square feet. When we calculating area the most important thing is that, all the dimensions must be in same units.

Conclusion

Understanding the concept of area involves knowing the specific formulas for different shapes, being able to apply these formulas correctly, and expressing the results in appropriate square units. This fundamental concept is widely used in various real-life situations, such as calculating the floor space of a room, the size of a plot of land, or the amount of material needed to cover a surface.