Polar Equation of a Circle

Polar form of the equation of the circle is almost similar to the parametric form of the equation of the circle. We usually write polar form of the equation of circle whose center is origin.

Let’s take a point P(rcosϴ, rsinϴ) on the boundary of the circle, where r is the distance of the point from origin.

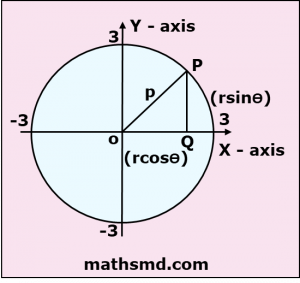
The equation of a circle centered at the origin and whose radius is p is

x² + y² = p².

To find the polar form of equation of a circle, put the value of x = rcosϴ and y = rsinϴ in the

x² + y² = p²

(rcos ϴ)² + (rsinϴ)² = p²

r ²cos ²ϴ + r ²sin ²ϴ =p²

r² (cos² ϴ + sin² ϴ) = p²

r² (cos² ϴ + sin² ϴ) = 1

(cos² ϴ + sin² ϴ) = 1 (trigonometry identity)

r² (1) = p²

r² = p²

r = p (where p is the radius of the circle)

This is the polar equation of a circle with radius r and center at the origin (0, 0).

Thus, the polar form is used to find the radius of the circle from the standard form of the equation of the circle.

Example: Find the radius of the standard equation by converting the following standard equation of a circle into polar form x² + y² = 9

Solution: To convert the standard equation of the circle into polar form,

Substitute the value of x = rcosϴ and

y = rsinϴ

Therefore, the standard equation of the circle becomes

(rcosϴ)² + (rsinϴ)² = 9

r²(cos²ϴ + sin²ϴ) = 9

We know that (cos²ϴ + sin²ϴ) = 1

putting the value we get

r² = 9

r = 3

Hence, the radius of the circle is 3cm. .