Fractions Multiplication with Different Denominators

Fractions that have different denominators are known as unlike fractions. Addition and subtraction of unlike fractions are different from addition and subtraction of like fractions, but the method of multiplication of unlike fractions and like fractions are same.

Multiplying fractions with different denominators is same as multiplication of common denominators.

The method of multiplication of fractions with different denominator is same as multiplication of two fractions.

First multiply the numerators, then multiply the denominators, and then fraction is reduced in its lowest form.

Let us understand this with an example.

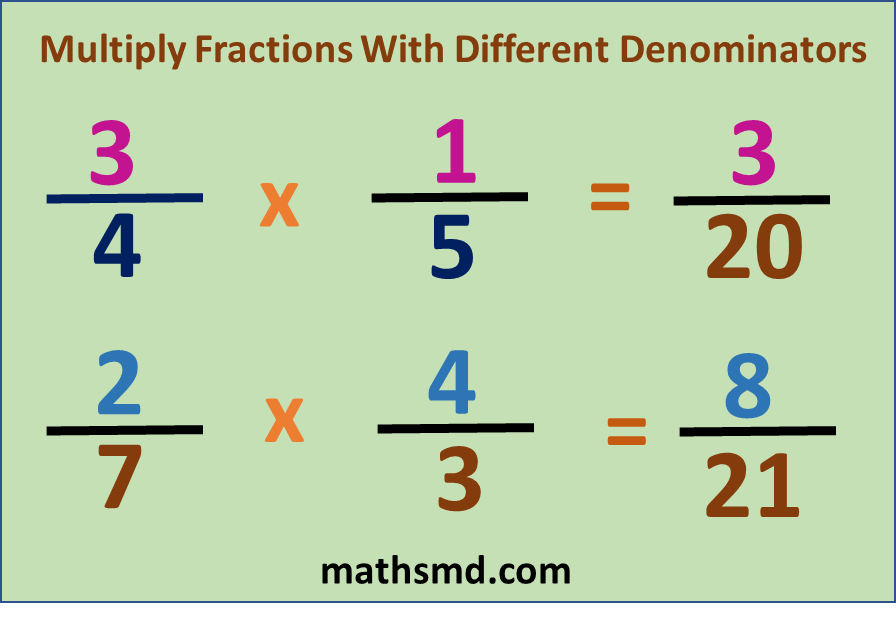
Example: Multiply 3/4 x 1/5

Here are steps given below.

Step 1: Multiply the numerators, 3 x 1 = 3

Step2 : Multiply denominators, 4 x 5 = 20

Step 3: The product of numerators is 3 and product of denominators is 20. So the product of

3/4 x 1/5 = 3/20

This cannot be reduced. Therefore, answer is 3/20.

Example: Multiply 2/7 x 4/3

Here are steps given below.

Step 1: Multiply the numerators, 2 x 4 = 8

Step2 : Multiply denominators, 7 x 3 = 21

Step 3: The product of numerators is 8 and product of denominators is 21. So the product of

2/7 x 4/3 = 8/21

This cannot be reduced. Therefore, answer is 8/21.