Diagonals of Polygon’s

In geometry, a line segment joining two vertices of a polygon or polyhedron, when those vertices are not adjacent is known as Diagonal.

 Diagonals of Polygon’s

A polygon’s diagonal’s are line segments, that joining from one corner to another corner.

Formula for number of diagonals = n(n-3)/2

where n is number of sides or vertices in a polygon.

Any quadrilateral has 4(4-3)/2 = 4 x 1/2 = 2 diagonals. 

A rectangle has  4(4-3)/2 = 4 x 1/2 = 2 diagonals.

                                 Rectangle

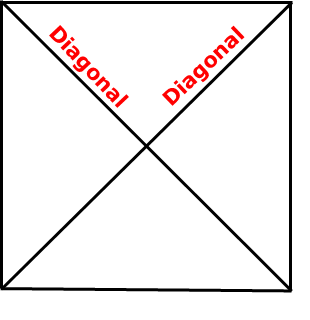
A square has 4(4-3)/2 = 4 x 1/2 = 2 diagonals.

                                  square

A parallelogram has 4(4-3)/2 = 4 x 1/2 = 2 diagonals.

                              Parallelogram

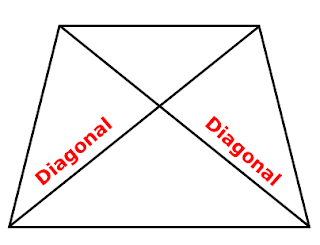
A trapezium has 4(4-3)/2 = 4 x 1/2 = 2 diagonals.

  Trapezium

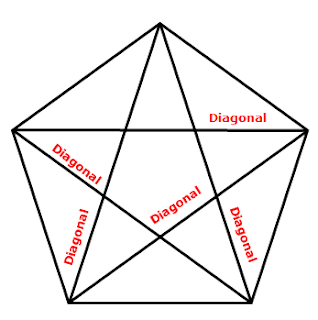
A pentagon has 5(5-3)/2 = 5 x 2/2 = 5 diagonals.

                             Pentagon

A hexagon has 6(6-3)/2 = 6 x 3/2 = 9 diagonals.

A octagon has 8(8-3)/2 = 8 x 5/2 = 20 diagonals.

A triangle has 3(3-3)/2 = 3 x 0/2 = 0 diagonals.