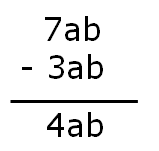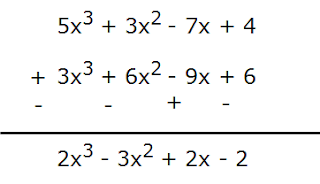Rules of Addition and Subtraction of like Terms 

In this lesson we will learn, how to add and subtract like terms

Like Terms

In an algebraic expression, like terms are terms that have same variables with same exponents and only the numerical coefficients of like terms are different.

The terms must have the same variables and the same exponents.

Example: 3x, 7x, 8x, 12x, x, -4x, -9x all are like terms because all terms has same variables, that is x and same exponent 1.

Let us look some examples to better understanding on addition and subtraction of algebraic expression with like terms.

When we simplify expressions or solve equations we need to combine like terms.

For example, expression 4x + 9y + 6x + 3x + 2y

When we solve the above expression first we combine like terms.

To combine like terms, the term must have the same variables and the same exponents and be sure that the + sign and – sign is in front of the coefficient or number in before the letter.

Here, 4x, 6x, and 3x have same variables,(x) and 9y, 2y have same variables(y).

In this example we will add the 4, 6 and 3, that is in front of x terms, then we will add 9 and 2 that is in front of y terms.

4x + 6x + 3x+ 9y + 2y

13x+ 11y

We can find the the sum of given polynomials, with either column method of addition or row method of addition.

Some more examples- 

              Row method of addition

Example 1: Add 2x + 5y + 3x+ 4y – 3y + 8x

Solution: 

Step 1: Rewrite the problem, so the like terms are next to each other.

                  2x + 3x + 8x  + 5y + 4y – 3y

Step 2: Combine the coefficients

                 (2 + 3 + 8)x  + (5 + 4 – 3)y

                             13x + 6y

Example 2: Add 2p + 3q + 6p+ 5q – 4q + 8p

Solution: Step 1: Rewrite the problem, so the like terms are next to each other.

                2p + 6p + 8p  + 3q + 5q – 4q 

Step 2: Combine the coefficients

               (2 + 6 + 8)p  + (3 + 5 – 4)q

                          16p + 4q


Example 3: Add (8x³ + 5x² – 7x + 4) and (3x³ – 2x² – 9x + 6)

Solution: Step 1: The given two polynomials are already in the arranged form, so we can write it as it is.8x³ + 5x² – 7x + 4 + 3x³ – 2x² – 9x + 6

Step 2: Now we write the like terms together starting from the highest power to lowest power. 8x³ + 3x³ + 5x² – 2x² – 7x – 9x + 4 + 6  so, the answer is,  11x³ + 3x² – 16x + 10

Example 4: Add 2(4x³ + 3x² – 5x + 8) and (9x³ – 12x² – 7x + 6)

Solution: = (8x³ + 6x² – 10x + 16) and (9x³ – 12x² – 7x + 6)
= 8x³ + 9x³ + 6x² – 12x² – 10x – 7x + 16 + 6

= 17x³ – 6x² – 17x + 22

Example 5: Add 3(4x⁴ + 2x³ – 3x² – 5x + 7) and (7x³ – 10x² – 5x + 6)

Solution:  = (12x⁴ + 6x³ – 9x² – 15x + 21) and (7x³ – 10x² – 5x + 6)
= 12x⁴ + 6x³ – 9x² – 15x + 21 + 7x³ – 10x² – 5x + 6
= 12x⁴ + 13x³ – 19x³ + 6x² – 12x² – 10x – 7x + 27 

^{= 17×3 – 6×2 – 17x + 22}  

Example 6: Add 3(2x³ + 6x² – 4x + 9) and 2(7x³ – 2x² + 5x – 8)

Solution: 
= 3(2x³ + 6x² – 4x + 9) and 2(7x³ – 2x² + 5x – 8)

= (6x³ + 18x² – 12x + 27) and (14x³ – 4x²  + 10x – 16) = 6x³ + 14x³ + 18x² – 4x² – 12x + 10x + 27 + 16

= 20x³ + 14x² – 2x + 43

Example 7: Add 3(2x⁵ + 6x⁴ – 7x³ – 3x² + 6x – 7) and 2(2x⁵ + 6x⁴ + 2x³ – 4x² + 7x – 8)

Solution: 

= 3(2x⁵ + 6x⁴ – 7x³ – 3x² + 6x – 7) + 2(2x⁵ + 6x⁴ + 2x³ – 4x² + 7x – 8)

= 6x⁵ + 18x⁴ – 21x³ – 9x² + 18x – 21 + 10x⁵ + 12x⁴ + 4x³ – 8x² + 14x – 16
= 6x⁵ + 10x⁵ + 18x⁴ + 12x⁴ – 21x³ + 4x³ – 9x² – 8x² + 18x + 14x – 21 – 16
= 16x⁵ + 30x⁴ – 17x³ – 17x² + 32x – 37

Example 8: Add –3(2x³ + 5x² – 2x + 6) and -2(5x³ – 2x² + 5x – 3)

Solution:
= -3(2x³ + 5x² – 2x + 6) + -2(5x³ – 2x²  + 5x – 3)
= -6x³ – 10x³ – 15x² + 4x² – 12x – 10x + 27 + 6
= 20x³ + 14x² – 2x + 43

           Column method of addition 

Example 1: Add  (5x³ + 3x² – 7x + 4) and (3x³ + 6x² – 9x + 6)

Solution: 
Step 1: First written in standard form as (5x³ + 3x² – 7x + 4) and (3x³ + 6x² – 9x + 6)

Step 2: Arrange like terms in columns.

Example 2: Add (6x³ + 2x² – 4x + 5) and (2x³ + 5x² – 9x + 7)

Solution: 
Step 1: First written in standard form as (6x³ + 2x² – 4x + 5) and (2x³ + 5x² – 9x + 7)

Step 2: Arrange like terms in columns

     

      Subtraction of like Terms

In this tutorial we will learn, subtraction of like terms. How to subtract like terms.

Example: 2y, 5y, 6y are like terms, because all terms has same variables, that is y, and same exponent 1.

Let us look some examples to better understanding on subtraction of algebraic expression with like terms.

When we simplify expressions or solve equations we need to combine like terms.

For example, expression 3a + 4b + 6b + 7a + 5b

When we solve the above expression, first we combine like terms.

To combine like terms, the term must have the same variables and the same exponents and be sure that the + sign and – sign is in front of the coefficient or number in before the letter.

Here, 3a, and 7a have same variables,(a terms) and 4b, 6b and 5b have same variables(b terms).

In this example we will add the 3 and 7, that is in front of a terms, then we will add 4, 6, and 5 that is in front of b terms.

We can solve the subtraction of a expression, with either column method of subtraction or row method of subtraction. 

Note: When adding or subtracting like terms, the coefficients are added or subtracted, and the variable remains same or unchanged. 

           Row method of subtraction

Example 1: Subtract (2a + 5b) from (7a – 3b).

Solution:  (7a – 3b) – (2a + 5b)

Step 1: Rewrite the problem, so the like terms are next to each other.

= 7a – 3b – 2a – 5b

Step 2: Combine the coefficients

= (7a – 2a) + (- 3b – 5b)

= 5a + (- 8b)

= 5a – 8b

Example 3: Subtract (2x³ + 5x² – 4x + 7) from (3x³ – 2x² – 6x + 8)

Solution: 
Step 1: The given two polynomials are already in the arranged form, so we can write it as it is.8x³ + 5x² – 7x + 4 + 3x³ – 2x² – 9x + 6 
Step 2: Now we write the like terms together starting from the highest power to lowest power. 8x³ + 3x³ + 5x² – 2x² – 7x – 9x + 4 + 6 

so, the answer is,  11x³ + 3x² – 16x + 10

      Column method of subtraction 

Example 3: Subtract 3ab from 7ab.

               7ab – 3ab = 4ab

Example 4: